题目内容
已知将一枚残缺不均匀的硬币连抛三次落在平地上,三次都正面朝上的概率为
.
(1)求将这枚硬币连抛三次,恰有两次正面朝上的概率;
(2)若将这枚硬币连抛两次之后,再另抛一枚质地均匀的硬币一次.在这三次抛掷中,正面朝上的总次数为ξ,求ξ的分布列及期望Eξ.
| 1 |
| 27 |
(1)求将这枚硬币连抛三次,恰有两次正面朝上的概率;
(2)若将这枚硬币连抛两次之后,再另抛一枚质地均匀的硬币一次.在这三次抛掷中,正面朝上的总次数为ξ,求ξ的分布列及期望Eξ.
(1)由题意知:将一枚硬币每抛一次正面朝上的概率P3=
,P=
…2分
设“这枚硬币连抛三次,恰有两次正面朝上”的事件为A,
则P(A)=
(1-P )=
•(
)2•(
) =
…4分
(2)ξ的取值情况可能为0,1,2,3,
P(ξ=0)=(
)2×
=
P(ξ=1)=2×
×
×
+(
)2×
=
P(ξ=2)=(
)2×
+2×
×
×
=
P(ξ=3)=(
)2×
=
…(8分)
∴ξ的分布列为
∴Eξ=0×
+1×
+2×
+3×
=
…(12分)
| 1 |
| 27 |
| 1 |
| 3 |
设“这枚硬币连抛三次,恰有两次正面朝上”的事件为A,
则P(A)=
| C | 23 |
| P | 2 |
| C | 23 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
(2)ξ的取值情况可能为0,1,2,3,
P(ξ=0)=(
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 9 |
P(ξ=1)=2×
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 4 |
| 9 |
P(ξ=2)=(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 5 |
| 18 |
P(ξ=3)=(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 18 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 2 |
| 9 |
| 4 |
| 9 |
| 5 |
| 18 |
| 1 |
| 18 |
| 7 |
| 6 |

练习册系列答案
相关题目
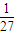 .
.