题目内容
设a,b∈R,且a≠b,a+b=2,则下列不等式成立的是( )
A.1<ab<
| B.ab<1<
| ||||
C.ab<
| D.
|
∵a+b=2,a≠b,∴ab<(
)2=1;
∵(a-b)2>0,∴
>ab;
∵2(a2+b2)>(a+b)2=4,
∴
>1.
综上可知:
>1>ab.
故选B.
| a+b |
| 2 |
∵(a-b)2>0,∴
| a2+b2 |
| 2 |
∵2(a2+b2)>(a+b)2=4,
∴
| a2+b2 |
| 2 |
综上可知:
| a2+b2 |
| 2 |
故选B.

练习册系列答案
相关题目


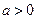 且
且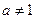 时,函数
时,函数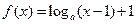 的图像恒过点
的图像恒过点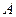 ,若点
,若点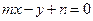 上,则
上,则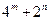 的最小值为
的最小值为 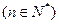 .
. ,则
,则 的最小值是( )
的最小值是( )
 ,且
,且 ,则
,则 的最大值为
的最大值为