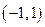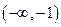题目内容
已知函数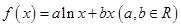 在点
在点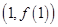 处的切线方程为
处的切线方程为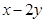
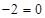 .
.
(1)求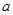 、
、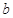 的值;
的值;
(2)当 时,
时,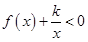 恒成立,求实数
恒成立,求实数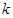 的取值范围;
的取值范围;
(3)证明:当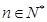 ,且
,且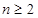 时,
时,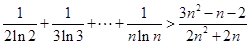 .
.
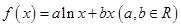 在点
在点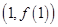 处的切线方程为
处的切线方程为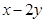
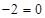 .
.(1)求
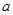 、
、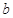 的值;
的值;(2)当
 时,
时,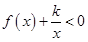 恒成立,求实数
恒成立,求实数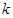 的取值范围;
的取值范围;(3)证明:当
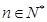 ,且
,且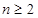 时,
时,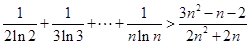 .
.(1)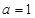 ,
,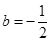 ;(2)
;(2)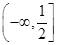 ;(3)详见解析.
;(3)详见解析.
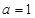 ,
,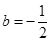 ;(2)
;(2)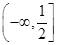 ;(3)详见解析.
;(3)详见解析.试题分析:(1)利用已知条件得到两个条件:一是切线的斜率等于函数
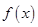 在
在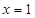 处的导数值
处的导数值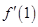 ,二是切点在切线上也在函数
,二是切点在切线上也在函数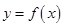 的图象上,通过切点
的图象上,通过切点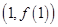 在切线上求出
在切线上求出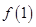 的值,然后再通过
的值,然后再通过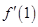 和
和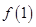 的值列有关
的值列有关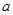 、
、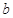 的二元一次方程组,求出
的二元一次方程组,求出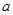 、
、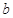 的值;(2)解法1是利用参数分离法将不等式
的值;(2)解法1是利用参数分离法将不等式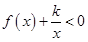 在区间
在区间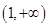 上恒成立问题转化为不等式
上恒成立问题转化为不等式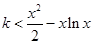 在区间
在区间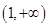 上恒成立,并构造函数
上恒成立,并构造函数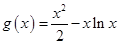 ,从而转化为
,从而转化为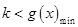 ,并利用导数求出函数
,并利用导数求出函数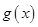 的最小值,从而求出
的最小值,从而求出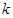 的取值范围;解法2是构造新函数
的取值范围;解法2是构造新函数 ,将不等式
,将不等式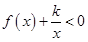 在区间
在区间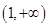 上恒成立问题转化为不等式
上恒成立问题转化为不等式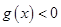 在区间
在区间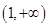 上恒成立问题,等价于
上恒成立问题,等价于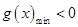 利用导数研究函数
利用导数研究函数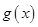 的单调性,对
的单调性,对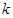 的取值进行分类讨论,通过在不同取值条件下确定函数
的取值进行分类讨论,通过在不同取值条件下确定函数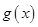 的单调性求出
的单调性求出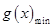 ,围绕
,围绕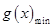
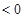 列不等式求解,从而求出
列不等式求解,从而求出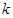 的取值范围;(3)在(2)的条件下得到
的取值范围;(3)在(2)的条件下得到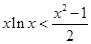 ,在不等式两边为正数的条件下两边取倒数得到
,在不等式两边为正数的条件下两边取倒数得到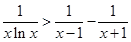 ,然后分别令
,然后分别令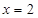 、
、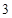 、
、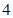 、
、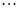 、
、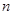 ,利用累加法以及同向不等式的相加性来证明问题中涉及的不等式.
,利用累加法以及同向不等式的相加性来证明问题中涉及的不等式.试题解析:(1)
 ,
, .
.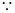 直线
直线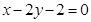 的斜率为
的斜率为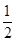 ,且过点
,且过点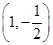 ,
, ,即
,即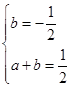 解得
解得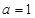 ,
,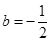 ;
;(2)解法1:由(1)得
 .
.当
 时,
时,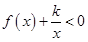 恒成立,即
恒成立,即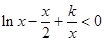 ,等价于
,等价于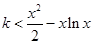 .
.令
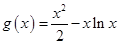 ,则
,则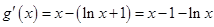 .
.令
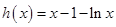 ,则
,则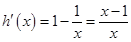 .
.当
 时,
时,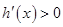 ,函数
,函数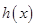 在
在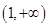 上单调递增,故
上单调递增,故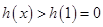 .
.从而,当
 时,
时,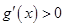 ,即函数
,即函数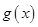 在
在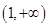 上单调递增,
上单调递增,故
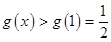 .
.因此,当
 时,
时,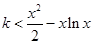 恒成立,则
恒成立,则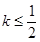 .
. 所求
所求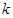 的取值范围是
的取值范围是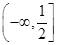 ;
;解法2:由(1)得
 .
.当
 时,
时,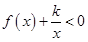 恒成立,即
恒成立,即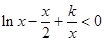 恒成立.
恒成立.令
 ,则
,则 .
.方程
 (*)的判别式
(*)的判别式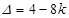 .
.(ⅰ)当
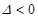 ,即
,即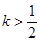 时,则
时,则 时,
时,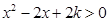 ,得
,得 ,
,故函数
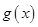 在
在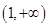 上单调递减.
上单调递减.由于
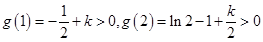 ,
,则当
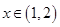 时,
时,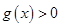 ,即
,即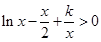 ,与题设矛盾;
,与题设矛盾;(ⅱ)当
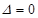 ,即
,即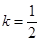 时,则
时,则 时,
时, .
.故函数
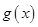 在
在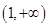 上单调递减,则
上单调递减,则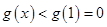 ,符合题意;
,符合题意;(ⅲ)当
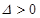 ,即
,即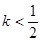 时,方程(*)的两根为
时,方程(*)的两根为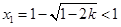 ,
,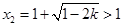 ,
,则
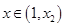 时,
时,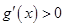 ,
,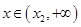 时,
时, .
.故函数
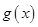 在
在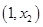 上单调递增,在
上单调递增,在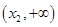 上单调递减,
上单调递减,从而,函数
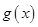 在
在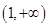 上的最大值为
上的最大值为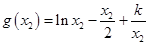 .
.而
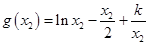
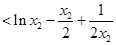 ,
,由(ⅱ)知,当
 时,
时, ,
,得
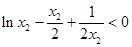 ,从而
,从而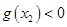 .
.故当
 时,
时,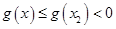 ,符合题意.
,符合题意.综上所述,
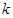 的取值范围是
的取值范围是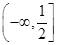 .
.(3)由(2)得,当
 时,
时, ,可化为
,可化为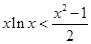 ,
,又
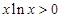 ,从而,
,从而,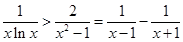 .
.把
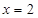 、
、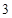 、
、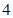 、
、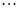 、
、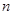 分别代入上面不等式,并相加得,
分别代入上面不等式,并相加得,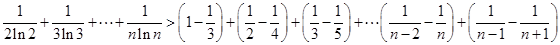
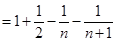
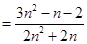 .
.
练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
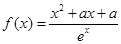 ,其
,其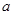 中为常数,
中为常数,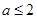 .
.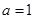 时,求曲线
时,求曲线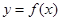 在点
在点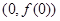 处的切线方程;
处的切线方程;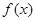 的极大值为
的极大值为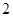 ?若存在,求出
?若存在,求出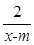 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若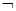 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围.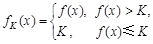 (K为给定常数),已知函数
(K为给定常数),已知函数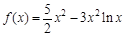 ,若对于任意的
,若对于任意的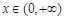 ,恒有
,恒有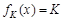 ,则实数K的取值范围为 .
,则实数K的取值范围为 .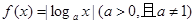 的单调递增区间是 .
的单调递增区间是 .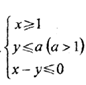 ,若函数z=x+y的最大值为4,则实数a的值为( )
,若函数z=x+y的最大值为4,则实数a的值为( )
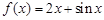 的部分图象可能是( )
的部分图象可能是( )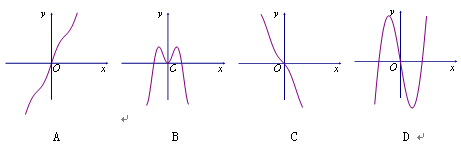
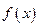 的定义域为R,
的定义域为R,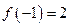 ,对任意
,对任意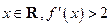 ,则
,则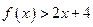 的解集为( )
的解集为( )