题目内容
已知椭圆![]() +
+![]() =1(a>b>0),过点A(a,0),B(0,b)的直线倾斜角为
=1(a>b>0),过点A(a,0),B(0,b)的直线倾斜角为![]() ,原点到该直线的距离为
,原点到该直线的距离为![]() .
.
(1)求椭圆的方程;
(2)是否存在实数k,使直线y=kx+2交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0).若存在,求出k的值;若不存在,请说明理由.
(1)由![]() =
=![]() ,
,![]() a·b=
a·b=![]() ·
·![]() ·
·![]() ,得a=
,得a=![]() ,b=1,所以椭圆方程是
,b=1,所以椭圆方程是![]() +y2=1.
+y2=1.
(2)存在.
将y![]() =kx+2代入
=kx+2代入![]() +y2=1,
+y2=1,
得(3k2+1)x2+12kx+9=0(*)
记P(x1,y1),Q(x2,y2),以PQ为直径的圆过D(1,0),则PD⊥QD,即(x1-1,y1)·(x2-1,y2)=(x1-1)(x2-1)+y1y2=0,又y1=kx1+2,y2=kx2+2,得
(k2+1)x1x2+(2k-1)(x1+x2)+5=0,
又x1x2=![]() ,x1+x2=-
,x1+x2=-![]() ,代入上式解得
,代入上式解得
k=-![]() ,
,
此时(*)方程Δ>0,∴存在k=-![]() ,满足题设条件.
,满足题设条件.

练习册系列答案
相关题目
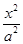 +
+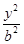 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 (
)
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 (
)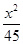 +
+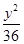 =1
B、
=1
B、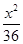 +
+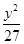 =1
=1 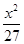 +
+ =1
D、
=1
D、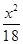 +
+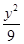 =1
=1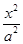 +
+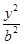 =1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( )
=1(a>b>0)的一个焦点是圆x2+y2-6x+8=0的圆心,且短轴长为8,则椭圆的左顶点为( ) 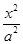 +
+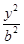 =1(a>b>0)的左右顶点为
=1(a>b>0)的左右顶点为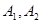 ,上下顶点为
,上下顶点为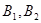 ,
左右焦点为
,
左右焦点为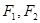 ,若
,若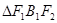 为等腰直角三角形(1)求椭圆的离心率(2)若
为等腰直角三角形(1)求椭圆的离心率(2)若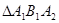 的面积为6
的面积为6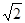 ,求椭圆的方程
,求椭圆的方程 +
+ =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P.若 =2
=2 ,则椭圆的离心率是( )
,则椭圆的离心率是( ) B.
B. C.
C. D.
D.