题目内容
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,AB=AA1,D,E,F分别为B1A,C1C,BC的中点,
(1)求证:DE∥平面ABC;
(2)求证:平面B1FA⊥平面AEF;
(3)求二面角B1-AE-F的大小。
(1)求证:DE∥平面ABC;
(2)求证:平面B1FA⊥平面AEF;
(3)求二面角B1-AE-F的大小。

解:以A为原点,以射线AB、AC、AA1分别为x、y、z的正半轴建立空间直角坐标系,
由AB=AC=AA1=2,
可知各点坐标分别为:A(0,0,0),B(2,0,0),C(0,2,0),
B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1),
(1)
设点G(-1,2,0),则 ,
,
∴ ,
,
 ,
, ,
,
∴DE∥平面ABC;
(2)证明: ,
,
∴ ,
,
 ,
,
∴ ,
,
又 ,
,
∴ ,
,
∵ ,
,
∴平面B1FA⊥平面AEF;
(3)由(2)可知 是平面AEF的一个法向量,
是平面AEF的一个法向量,
设二面角B1-AE-F的大小为θ,根据已知得θ为锐角,
设平面AEB1的一个法向量为 ,
,
 ,
,
∴ ,解得
,解得 ,
,
∴ ,
,
∴ ,
,
∴ ,
,
∴ ,
,
∴二面角B1-AE-F的大小为 。
。
由AB=AC=AA1=2,
可知各点坐标分别为:A(0,0,0),B(2,0,0),C(0,2,0),
B1(2,0,2),E(0,2,1),F(1,1,0),D(1,0,1),
(1)

设点G(-1,2,0),则
 ,
,∴
 ,
, ,
, ,
,∴DE∥平面ABC;
(2)证明:
 ,
,∴
 ,
, ,
,∴
 ,
,又
 ,
,∴
 ,
,∵
 ,
,∴平面B1FA⊥平面AEF;
(3)由(2)可知
 是平面AEF的一个法向量,
是平面AEF的一个法向量,设二面角B1-AE-F的大小为θ,根据已知得θ为锐角,
设平面AEB1的一个法向量为
 ,
, ,
,∴
 ,解得
,解得 ,
,∴
 ,
,∴
 ,
,∴
 ,
,∴
 ,
,∴二面角B1-AE-F的大小为
 。
。
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.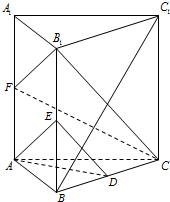 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.