题目内容
（2013•惠州一模）在△ABC中，角A，B，C所对的边分别为a，b，c且满足csinA=acosC．
（I）求角C的大小；
（II）求
sinA-cos(B+C)的最大值，并求取得最大值时角A，B的大小．
（I）求角C的大小；
（II）求
| 3 |
分析：（I）在△ABC中，利用正弦定理将csinA=acosC化为sinCsinA=sinAcosC，从而可求得角C的大小；
（II）利用两角和的余弦与辅助角公式可将
sinA-cos（B+C）化为
sinA-cos（B+C）=2sin（A+
），从而可求取得最大值时角A，B的大小．
（II）利用两角和的余弦与辅助角公式可将
| 3 |
| 3 |
| π |
| 6 |
解答：解析：（I）由正弦定理得sinCsinA=sinAcosC，
∵0＜A＜π，
∴sinA＞0，
∴sinC=cosC，又cosC≠0，
∴tanC=1，又C是三角形的内角
即∠C=
…（4分）
（II）
sinA-cos（B+C）=
sinA-cos（π-A）
=
sinA+cosA=2sin（A+
）…（7分）
又0＜A＜
，
＜A+
＜
，
所以A+
=
即A=
时，2sin（A+
）取最大值2． （10分）
综上所述，
sinA-cos（B+C）的最大值为2，此时A=
，B=
…（12分）
∵0＜A＜π，
∴sinA＞0，
∴sinC=cosC，又cosC≠0，
∴tanC=1，又C是三角形的内角
即∠C=
| π |
| 4 |
（II）
| 3 |
| 3 |
=
| 3 |
| π |
| 6 |
又0＜A＜
| 3π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 11π |
| 12 |
所以A+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
综上所述，
| 3 |
| π |
| 3 |
| 5π |
| 12 |
点评：本题考查正弦定理，考查两角和的余弦与辅助角公式，考查求三角函数的最值，掌握三角函数的基本关系是化简的基础，属于中档题．
练习册系列答案
天天向上口算本系列答案
相关题目
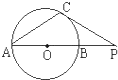（2013•惠州一模）（几何证明选做题）