题目内容
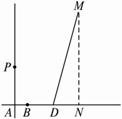
如图,平面上两条直线AB与AP互相垂直,AB=1,AP=3,D在直线AB上,AD=4,平面上动点M在直线AB上的射影为点N,满足DM=2BN.(1)求动点M的轨迹C的方程;
(2)若直线y=kx+M(k≠0,M≠0)与点M的轨迹C交于不同的两点E、F,且E、F都在以P为圆心的圆上,求实数M的取值范围.
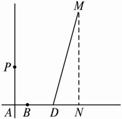
解：(1)以A为原点，AB所在直线为x轴建立平面直角坐标系，则B(1，0)，D(4，0)，P(0，3)，?
设M(x,y),则N(x,0), ?
由|DM|=2|BN|，得
=2|x-1|,?
整理得点M的轨迹方程为
=1. ?
(2)设E(x1,y1),F(x2,y2),?
由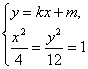
消去y整理得(3-k2)x2-2kMx-(M2+12)=0.?
依题意得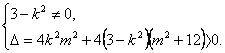
(*) ?
设EF的中点为G(x0,y0),则x0=
=
.?
∵点G在直线y=kx+M上,∴y0=kx0+M=
.?
∴G(
,
). ?
∵E、F两点都在以P(0,3)为圆心的同一圆上，?
∴GP⊥EF，即kGP·k=-1.?
∴
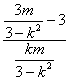·k=-1,整理得k2=
. ?
代入(*)式得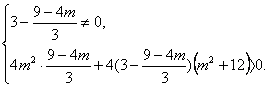
?
解得M＞0或M＜-
. ?
又k2=
＞0，∴M＜
.?
故所求M的取值范围是(-∞,-
)∪(0,
).
小学教材完全解读系列答案
10、如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p、q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题：
如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若p、q分别是M到直线l1和l2的距离，则称有序非负实数对（p，q）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列命题①若p=q=0，则“距离坐标”为（0，0）的点有且仅有1个；
如图，平面中两条直线l1和l2相交于点O，对于平面上任意一点M，若x，y分别是M到直线l1和l2的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：