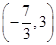题目内容
若关于x的不等式|2x-4|+|4x-2|>a恒成立,求a的取值范围.分析:去绝对值号,分段求出不等式左侧表达式取值范围,然后求其在R上的最小值,令a小于其最小值,即得a的取值范围.
解答:解:令g(x)=|2x-4|+|4x-2|,a<gmin(x)即可
g(x)=
,
当x=
时,g(x)取最小值3a<gmin(x)即可,故a<3.(10分)
g(x)=
|
当x=
| 1 |
| 2 |
点评:考查分段函数值域的求法,及不等式恒成立求参数的技巧.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
若关于x的不等式2-x2>|x-a|至少有一个负数解,则a的取值范围为( )
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(-
|
 >|x-a|
至少有一个负数解,则实数a的取值范围是
.
>|x-a|
至少有一个负数解,则实数a的取值范围是
. >|x-a| 至少有一个负数解,则a的取值范围为(
)
>|x-a| 至少有一个负数解,则a的取值范围为(
) B.
B.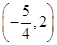 C.
C.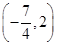 D.
D.