题目内容
已知双曲线C的方程为：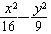
=1，
（1）求双曲线C的顶点坐标和离心率；
（2）设双曲线C的右准线与其中一条渐近线相交于点D，点F为双曲线的右焦点，证明△ODF为直角三角形（O为坐标原点）。
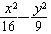=1，（1）求双曲线C的顶点坐标和离心率；
（2）设双曲线C的右准线与其中一条渐近线相交于点D，点F为双曲线的右焦点，证明△ODF为直角三角形（O为坐标原点）。
解：（1）∵a=4，b=3，c=5，
∴双曲线顶点的坐标为（±4，0），离心率e=
；
（2）F（5，0），右准线方程为x=
、一条渐近线方程为y=
x，
解方程组
，得D（
，
），
kFD=
，kOD=
，kFD·kOD=-1，
所以△ODF为直角三角形。
∴双曲线顶点的坐标为（±4，0），离心率e=
；（2）F（5，0），右准线方程为x=
、一条渐近线方程为y=x，解方程组
，得D（，），kFD=
，kOD=，kFD·kOD=-1，所以△ODF为直角三角形。
练习册系列答案
相关题目