题目内容
已知二次函数f(x)=x2-ax+a,(a≠0x∈R),有且仅有唯一的实数x满足f(x)≤0.
(1)在数列{an}中,满足Sn=f(n)-4,求{an}的通项;
(2)在数列{an}中依次取出第1项、第2项、第4项、…第2n-1项…组成新数列{bn},求新数列的前n项和Tn;
(3)设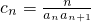 ,求数列{cn}的最大和最小值.
,求数列{cn}的最大和最小值.
解:(1)∵f(x)≤0有且仅有唯一的实数x满足,
∴△=a2-4a=0,∴a=0或a=4.
∵a≠0,∴a=4.
Sn=f(n)-4=n2-4n,
当n=1时,a1=S1=-3,
当n≥2时,an=Sn-Sn-1=2n-5,且对n=1也符合,∴an=2n-5.
(2)bn=2×2n-1-5=2n-5
∴Tn=(2+4+…+2n)-5n
=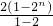 -5n
-5n
=2n+1-5n-2.
(3)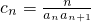 =
= =
=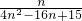 =
=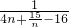
 ,c2=-2,
,c2=-2,
当n≥3时,4(n+1)+ -(4n+
-(4n+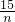 )=4-
)=4- >0,4n+
>0,4n+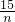 单调递增,且4n+
单调递增,且4n+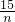 -16>0,
-16>0,
数列{cn}的最大值为c3=1最小值c2=-2.
分析:(1)根据二次函数的图象与性质,可得出△=a2-4a=0,解出a,再利用数列中an与 Sn关系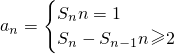 求出{an}的通项.
求出{an}的通项.
(2)由(1)可以求出an=2n-5,从而bn=2×2n-1-5=2n-5,利用公式法及分组法求出Tn;
(3)cn=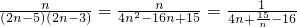 利用4n+
利用4n+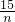 单调性解决cn的最值.
单调性解决cn的最值.
点评:本题考查二次函数的图象与性质,数列通项公式求解,数列公式法、分组法求和,数列的函数性质.考查推理论证、计算能力,分类讨论的思想.
∴△=a2-4a=0,∴a=0或a=4.
∵a≠0,∴a=4.
Sn=f(n)-4=n2-4n,
当n=1时,a1=S1=-3,
当n≥2时,an=Sn-Sn-1=2n-5,且对n=1也符合,∴an=2n-5.
(2)bn=2×2n-1-5=2n-5
∴Tn=(2+4+…+2n)-5n
=
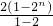 -5n
-5n=2n+1-5n-2.
(3)
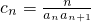 =
= =
=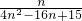 =
=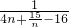
 ,c2=-2,
,c2=-2,当n≥3时,4(n+1)+
 -(4n+
-(4n+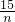 )=4-
)=4- >0,4n+
>0,4n+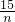 单调递增,且4n+
单调递增,且4n+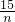 -16>0,
-16>0,数列{cn}的最大值为c3=1最小值c2=-2.
分析:(1)根据二次函数的图象与性质,可得出△=a2-4a=0,解出a,再利用数列中an与 Sn关系
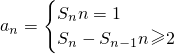 求出{an}的通项.
求出{an}的通项.(2)由(1)可以求出an=2n-5,从而bn=2×2n-1-5=2n-5,利用公式法及分组法求出Tn;
(3)cn=
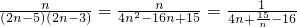 利用4n+
利用4n+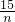 单调性解决cn的最值.
单调性解决cn的最值.点评:本题考查二次函数的图象与性质,数列通项公式求解,数列公式法、分组法求和,数列的函数性质.考查推理论证、计算能力,分类讨论的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目