Question

一个工厂在某年里每月产品的总成本y（万元）与该月产量x（万件）之间有如下一组对应数据：

x	1.08	1.12	1.19	1.28	1.36	1.48	1.59	1.68	1.80	1.87	1.98	2.07
y	2.25	2.37	2.40	2.55	2.64	2.75	2.92	3.03	3.14	3.26	3.36	3.50

（1）画出散点图；

（2）求月总成本y与月总产量x之间的回归直线方程.

Answer 1

解：（1）

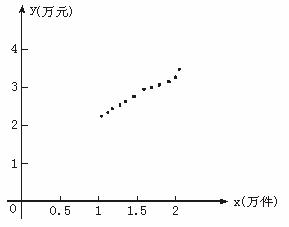
（2）经计算可得

=，==2.8475，x_i²=29.808，y_i²=99.2081，x_iy_i=54.243.

b=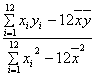=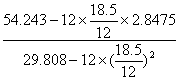≈1.215.

a=－b=2.8475－1.215×≈0.974.

故所求的回归直线方程为=1.215x+0.974.

点评：对一组数据进行线性回归分析时，应先画出其散点图，看其是否呈直线形，再依系数a、b的计算公式，算出a、b.由于计算量较大，所以在计算时应借助技术手段，认真细致，谨防计算中产生错误.