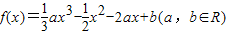题目内容
已知函数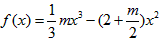 +4x+1,g(x)=mx+5。
+4x+1,g(x)=mx+5。
(1)当m≥4时,求f(x)的单调递增区间;
(2)是否存在m<0,使得对任意的x1,x2∈[2,3],都有f(x1)-g(x2)≤1恒成立,若存在,求出m的取值范围;若不存在,请说明理由。
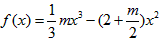 +4x+1,g(x)=mx+5。
+4x+1,g(x)=mx+5。 (1)当m≥4时,求f(x)的单调递增区间;
(2)是否存在m<0,使得对任意的x1,x2∈[2,3],都有f(x1)-g(x2)≤1恒成立,若存在,求出m的取值范围;若不存在,请说明理由。
解:(1)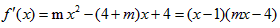 ,
,
当m=4时,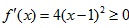 ,
,
∴f(x)在(-∞,+∞)上单增,
当m>4时,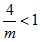 ,
,
∴f(x)的递增区间为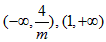 ;
;
(2)假设存在m<0,使得命题成立,此时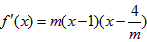 ,
,
∵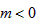 ,
,
∴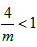 ,
,
则f(x)在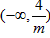 和(1,+∞)递减,在
和(1,+∞)递减,在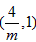 递增,
递增,
∴f(x)在[2,3]上单减,
又g(x)在[2,3]单减,
∴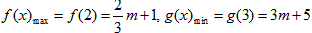 ,
,
因此,对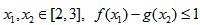 恒成立,
恒成立,
即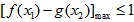 ,
,
亦即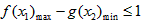 恒成立,
恒成立,
∴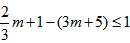
∴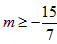 ,
,
又m<0,故m的范围为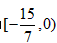 。
。
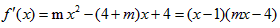 ,
,当m=4时,
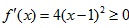 ,
, ∴f(x)在(-∞,+∞)上单增,
当m>4时,
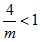 ,
,∴f(x)的递增区间为
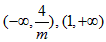 ;
;(2)假设存在m<0,使得命题成立,此时
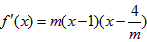 ,
,∵
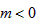 ,
, ∴
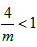 ,
,则f(x)在
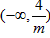 和(1,+∞)递减,在
和(1,+∞)递减,在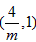 递增,
递增,∴f(x)在[2,3]上单减,
又g(x)在[2,3]单减,
∴
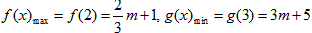 ,
,因此,对
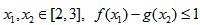 恒成立,
恒成立,即
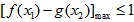 ,
, 亦即
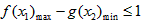 恒成立,
恒成立,∴
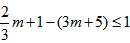
∴
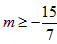 ,
,又m<0,故m的范围为
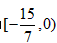 。
。 
练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目