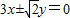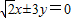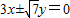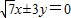题目内容
若F1、F2是双曲线
＝1的两个焦点，P在双曲线上，且|PF1|·|PF2|＝32，求∠F1PF2的大小．
答案：
解析：
解析：
|
解：由双曲线的对称性，可设点P在第一象限，由双曲线的方程，知a＝3，b＝4．∴c＝5． 由双曲线的定义，得|PF1|－|PF2|＝2a＝6． 上式两边平方，得|PF1|2＋|PF2|2＝36＋2|PF1|·|PF2|＝36＋64＝100， 由余弦定理，得 cos∠F1PF2＝ ∴∠F1PF2＝90°． 分析：一般地，求一个角的大小，通常要解这个角所在的三角形． |
＝0．
练习册系列答案
阅读快车系列答案
相关题目
=1的两个焦点,P在双曲线上,且|PF1|·|PF2|=32,求∠F1PF2的大小.
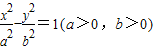与椭圆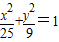
的共同焦点，点P是两曲线的一个交点，且△PF1F2为等腰三角形，则该双曲线的渐近线方程是（ ）
