题目内容
在△ABC中，若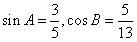
，判断△ABC的形状，求出cosC的值。
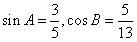，判断△ABC的形状，求出cosC的值。解：∵
＞0，
∴sinB=
，
又sinA=
，
∴sinA＜sinB，由正弦定理得a＜b，
由大边对大角得A＜B，
∴A为锐角，
∴cosC=-cos（A+B）=-（cosAcosB-sinAsinB）=
＞0，
∴C也为锐角，
∴△ABC为锐角三角形且cosC=
。
＞0，∴sinB=
，又sinA=
， ∴sinA＜sinB，由正弦定理得a＜b，
由大边对大角得A＜B，
∴A为锐角，
∴cosC=-cos（A+B）=-（cosAcosB-sinAsinB）=
＞0， ∴C也为锐角，
∴△ABC为锐角三角形且cosC=
。 
练习册系列答案
名师金手指领衔课时系列答案
相关题目
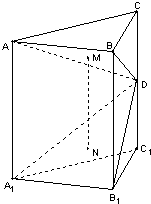如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，BC=AC=2，AA1=4，D为棱CC1上的一动点，M、N分别为△ABD，△A1B1D的重心．
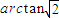，求点C1到平面A1B1D的距离；