题目内容
如图,在三棱柱 中,AC⊥BC,AB⊥
中,AC⊥BC,AB⊥ ,
,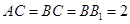 ,D为AB的中点,且CD⊥
,D为AB的中点,且CD⊥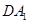 。
。
(Ⅰ)求证:平面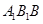 ⊥平面ABC;
⊥平面ABC;
(2)求多面体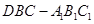 的体积。
的体积。
(Ⅰ)详见解析;(Ⅱ)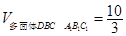 .
.
解析试题分析:(Ⅰ)求证:平面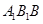 ⊥平面
⊥平面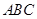 ,只需证明一个平面过另一个平面的垂线,即找线面垂直,由已知
,只需证明一个平面过另一个平面的垂线,即找线面垂直,由已知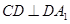 ,可考虑在平面
,可考虑在平面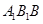 ,即面
,即面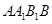 内找一条直线与
内找一条直线与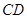 垂直,问题得证,由已知
垂直,问题得证,由已知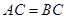 ,
,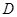 为
为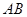 的中点,则
的中点,则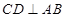 ,这样
,这样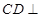 面
面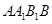 ,从而得证;(Ⅱ)求多面体
,从而得证;(Ⅱ)求多面体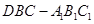 的体积,这是一个不规则的几何体,要求它的体积,需要分割,即把它分割成规则的几何体,从而求出体积,由图可知,它是三棱柱
的体积,这是一个不规则的几何体,要求它的体积,需要分割,即把它分割成规则的几何体,从而求出体积,由图可知,它是三棱柱 ,去掉三棱锥
,去掉三棱锥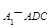 ,由已知三棱柱
,由已知三棱柱 是直三棱柱,故
是直三棱柱,故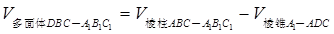 ,可求得体积.
,可求得体积.
试题解析:(Ⅰ)∵AC=BC,D为AB的中点,
∴CD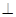 AB,又CD
AB,又CD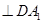 ,∴CD
,∴CD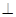 面
面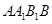 ,
,
又因为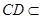 平面ABC,故平面
平面ABC,故平面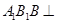 平面
平面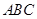 。(6分)
。(6分)
(Ⅱ)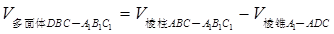
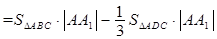
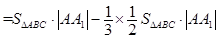
 .(12分)
.(12分)
考点:面面垂直的判定,几何体的体积.

练习册系列答案
相关题目
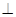 底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且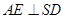
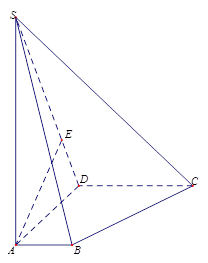
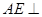 平面
平面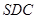 ;
;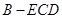 的体积
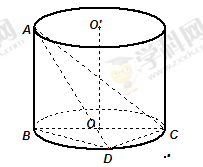
的体积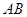 是圆柱体
是圆柱体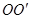 的一条母线,
的一条母线,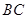 过底面圆的圆心
过底面圆的圆心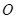 ,
,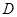 是圆
是圆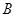 、
、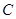 重合的任意一点,已知棱
重合的任意一点,已知棱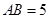 ,
,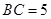 ,
,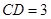 .
.
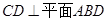 ;
;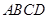 绕母线
绕母线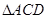 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.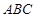 中,
中,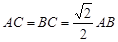 ,
,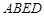 是边长为
是边长为 的正方形,平面
的正方形,平面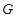 、
、 分别是
分别是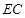 、
、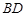 的中点.
的中点.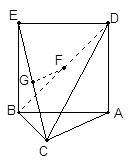
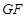 ∥底面
∥底面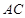 ⊥平面
⊥平面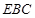 ;
;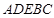 的体积.
的体积.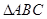 中,
中,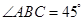 ,
,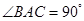 ,
,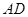 是
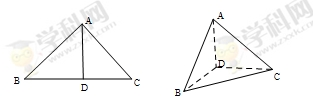
是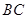 上的高,沿
上的高,沿 折起,使
折起,使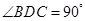 .
.
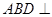 平面
平面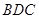 ;
;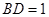 ,求三棱锥
,求三棱锥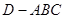 的体积.
的体积.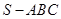 中,
中,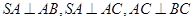 且
且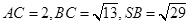 .
.
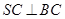 ;
;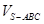 .
. 的底面边长为
的底面边长为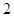 ,侧棱长为
,侧棱长为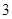 ,
,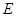 为棱
为棱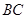 的中点.
的中点.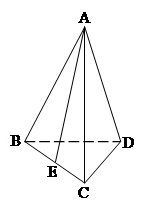
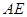 与
与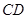 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);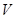 .
.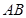 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.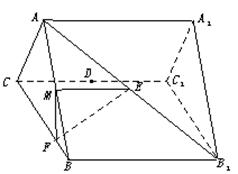
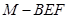 的体积.
的体积.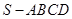 中,侧棱
中,侧棱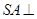 底面
底面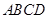 ,且底面
,且底面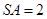 ,
,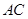 与
与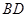 相交于点
相交于点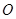 .
.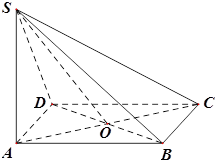
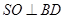 ;
;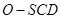 的体积.
的体积.