题目内容
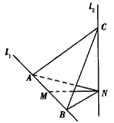
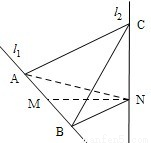
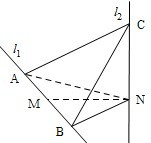如图，l1、l2是互相垂直的异面直线，MN是它们的公垂线段．点A、B在l1上，C在l2上，AM=MB=MN．（Ⅰ）证明AC⊥NB；
（Ⅱ）若∠ACB=60°，求NB与平面ABC所成角的余弦值．
分析：（1）欲证AC⊥NB，可先证BN⊥面ACN，根据线面垂直的判定定理只需证AN⊥BN，CN⊥BN即可；
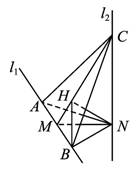
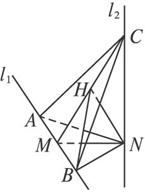
（2）易证N在平面ABC内的射影H是正三角形ABC的中心，连接BH，∠NBH为NB与平面ABC所成的角，在Rt△NHB中求出此角即可．
（2）易证N在平面ABC内的射影H是正三角形ABC的中心，连接BH，∠NBH为NB与平面ABC所成的角，在Rt△NHB中求出此角即可．
解答：
解：（Ⅰ）由已知l2⊥MN，l2⊥l1，MN∩l1=M，可得l2⊥平面ABN．
由已知MN⊥l1，AM=MB=MN，
可知AN=NB且AN⊥NB．又AN为AC在平面ABN内的射影．
∴AC⊥NB
（Ⅱ）∵Rt△CAN≌Rt△CNB，
∴AC=BC，又已知∠ACB=60°，
因此△ABC为正三角形．
∵Rt△ANB≌Rt△CNB，
∴NC=NA=NB，因此N在平面ABC内的射影H是正三角形ABC的中心，
连接BH，∠NBH为NB与平面ABC所成的角．
在Rt△NHB中，cos∠NBH=
=
=
．
解：（Ⅰ）由已知l2⊥MN，l2⊥l1，MN∩l1=M，可得l2⊥平面ABN．由已知MN⊥l1，AM=MB=MN，
可知AN=NB且AN⊥NB．又AN为AC在平面ABN内的射影．
∴AC⊥NB
（Ⅱ）∵Rt△CAN≌Rt△CNB，
∴AC=BC，又已知∠ACB=60°，
因此△ABC为正三角形．
∵Rt△ANB≌Rt△CNB，
∴NC=NA=NB，因此N在平面ABC内的射影H是正三角形ABC的中心，
连接BH，∠NBH为NB与平面ABC所成的角．
在Rt△NHB中，cos∠NBH=
| HB |
| NB |
| ||||
|
| ||
| 3 |
点评：本题主要考查了直线与平面之间的位置关系，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
