题目内容
已知f(x)= ax3-2x2+cx的导函数的值域为[0,+∞),是
ax3-2x2+cx的导函数的值域为[0,+∞),是 的最小值为
的最小值为
- A.0
- B.

- C.

- D.1
C
分析:先求函数的导函数f′(x)=ax2-4x+c,由导函数的值域为[0,+∞),可得a>0,且ac=4,利用均值定理a+c≥2 =4,再将所求代数式通分化简为关于(a+c)的函数,最后设t=a+c利用换元法,结合导数求得函数的最小值
=4,再将所求代数式通分化简为关于(a+c)的函数,最后设t=a+c利用换元法,结合导数求得函数的最小值
解答:f(x)= ax3-2x2+cx的导数为f′(x)=ax2-4x+c
ax3-2x2+cx的导数为f′(x)=ax2-4x+c
∵导函数的值域为[0,+∞),
∴
解得:
∵ =
= =
= =
=
= =
= =
=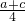 -
-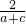
设t=a+c≥2 =4,∴t∈[4,+∞)
=4,∴t∈[4,+∞)
∴ =
=
设g(t)= t∈[4,+∞)
t∈[4,+∞)
g′(t)= +
+ >0,
>0,
∴g(t)在 t∈[4,+∞)为增函数
∴g(t)∈[ ,+∞)
,+∞)
∴ 的最小值为
的最小值为
故选C
点评:本题考察了导函数的求法,二次函数图象和性质,均值定理的应用以及换元法求函数的值域的方法
分析:先求函数的导函数f′(x)=ax2-4x+c,由导函数的值域为[0,+∞),可得a>0,且ac=4,利用均值定理a+c≥2
 =4,再将所求代数式通分化简为关于(a+c)的函数,最后设t=a+c利用换元法,结合导数求得函数的最小值
=4,再将所求代数式通分化简为关于(a+c)的函数,最后设t=a+c利用换元法,结合导数求得函数的最小值解答:f(x)=
 ax3-2x2+cx的导数为f′(x)=ax2-4x+c
ax3-2x2+cx的导数为f′(x)=ax2-4x+c∵导函数的值域为[0,+∞),
∴

解得:

∵
 =
= =
= =
=
=
 =
= =
=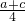 -
-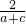
设t=a+c≥2
 =4,∴t∈[4,+∞)
=4,∴t∈[4,+∞)∴
 =
=
设g(t)=
 t∈[4,+∞)
t∈[4,+∞)g′(t)=
 +
+ >0,
>0,∴g(t)在 t∈[4,+∞)为增函数
∴g(t)∈[
 ,+∞)
,+∞)∴
 的最小值为
的最小值为
故选C
点评:本题考察了导函数的求法,二次函数图象和性质,均值定理的应用以及换元法求函数的值域的方法

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |