题目内容
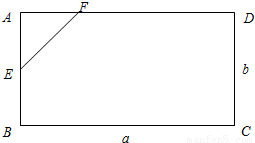
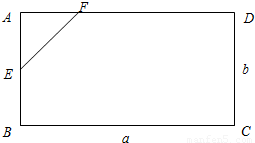
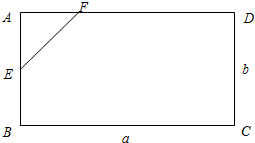 第八届中国花博会将于2013年9月在常州举办,展览园指挥中心所用地块的形状是大小一定的矩形ABCD,BC=a,CD=b.a,b为常数且满足b<a.组委会决定从该矩形地块中划出一个直角三角形地块AEF建游客休息区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为(l>2b),如图.设AE=x,△AEF的面积为S.
第八届中国花博会将于2013年9月在常州举办,展览园指挥中心所用地块的形状是大小一定的矩形ABCD,BC=a,CD=b.a,b为常数且满足b<a.组委会决定从该矩形地块中划出一个直角三角形地块AEF建游客休息区(点E,F分别在线段AB,AD上),且该直角三角形AEF的周长为(l>2b),如图.设AE=x,△AEF的面积为S.(1)求S关于x的函数关系式;
(2)试确定点E的位置,使得直角三角形地块AEF的面积S最大,并求出S的最大值.
分析:(1)根据题意,分析可得,欲求,△AEF场地占地面积,只须求出图中直角三角形的周长求出另一边长AF,再结合直角三角形的面积计算公式求出它们的面积即得;
(2)对于(1)所列不等式,可利用导数研究它的单调性求它的最大值,从而解决问题.
(2)对于(1)所列不等式,可利用导数研究它的单调性求它的最大值,从而解决问题.
解答:解:(1)设AF=y,则x+y+
=l,
整理,得y=
.…(3分)
S=
xy=
,x∈(0,b]. …(4分)
(2)S′=
•
=
(x-
l)•(x-
l),x∈(0,b]
∴当b≤
l时,S′>0,S在(0,b]递增,
故当x=b时,Smax=
;
当b>
l时,在x∈(0,
l)上,S′>0,S递增,在x∈(
l,b)上,S′<0,S递减,
故当x=
l时,Smax=
l2.
| x2+y2 |
整理,得y=
| l2-2lx |
| 2(l-x) |
S=
| 1 |
| 2 |
| x(l2-2lx) |
| 4(l-x) |
(2)S′=
| l |
| 4 |
| 2x2-4lx+l2 |
| (x-l)2 |
| 2l |
| 4(x-l)2 |
2-
| ||
| 2 |
2+
| ||
| 2 |
∴当b≤
2-
| ||
| 2 |
故当x=b时,Smax=
| bl(2b-l) |
| 4(b-l) |
当b>
2-
| ||
| 2 |
2-
| ||
| 2 |
2-
| ||
| 2 |
故当x=
2-
| ||
| 2 |
3-2
| ||
| 4 |
点评:本小题主要考查函数模型的选择与应用、函数解析式的求解及常用方法及导数的应用等基础知识,属于基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目