题目内容
已知等差数列{an}的前n项和为Sn,且S10=55,S20=210.
(1)求数列{an}的通项公式;
(2)设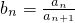 ,是否存在m、k(k>m≥2,k,m∈N*),使得b1、bm、bk成等比数列.若存在,求出所有符合条件的m、k的值;若不存在,请说明理由.
,是否存在m、k(k>m≥2,k,m∈N*),使得b1、bm、bk成等比数列.若存在,求出所有符合条件的m、k的值;若不存在,请说明理由.
解:(1)设等差数列{an}的公差为d,则 .(1分)
.(1分)
由已知,得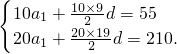 (3分)
(3分)
即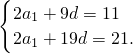 解得
解得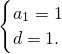 (5分)
(5分)
所以an=a1+(n-1)d=n(n∈N*).(6分)
(2)假设存在m、k(k>m≥2,m,k∈N),使得b1、bm、bk成等比数列,
则bm2=b1bk.(7分)
因为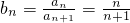 ,(8分)
,(8分)
所以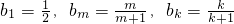 .
.
所以 .(9分)
.(9分)
整理,得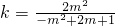 .(10分)
.(10分)
因为k>0,所以-m2+2m+1>0.(11分)
解得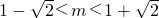 .(12分)
.(12分)
因为m≥2,m∈N*,
所以m=2,此时k=8.
故存在m=2、k=8,使得b1、bm、bk成等比数列.(14分)
分析:(1)设出其首项和公差,直接利用S10=55,S20=210求出首项和公差即可求数列{an}的通项公式;
(2)先求出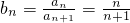 ,再代入b1、bm、bk成等比数列对应的等量关系,求出m、k之间的关系式,再利用题中k>m≥2,k,m∈N*,即可求出对应的m、k的值.
,再代入b1、bm、bk成等比数列对应的等量关系,求出m、k之间的关系式,再利用题中k>m≥2,k,m∈N*,即可求出对应的m、k的值.
点评:本题第一问主要考查利用等差数列的前n项和求数列{an}的通项公式以及等比关系的确定,是对等差数列,等比数列基础知识的考查.作这一类型题目,一般是设出基本量,利用已知条件列出等量关系,再进行求解即可.
 .(1分)
.(1分)由已知,得
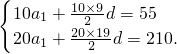 (3分)
(3分)即
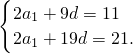 解得
解得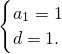 (5分)
(5分)所以an=a1+(n-1)d=n(n∈N*).(6分)
(2)假设存在m、k(k>m≥2,m,k∈N),使得b1、bm、bk成等比数列,
则bm2=b1bk.(7分)
因为
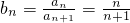 ,(8分)
,(8分)所以
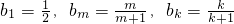 .
.所以
 .(9分)
.(9分)整理,得
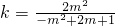 .(10分)
.(10分)因为k>0,所以-m2+2m+1>0.(11分)
解得
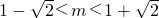 .(12分)
.(12分)因为m≥2,m∈N*,
所以m=2,此时k=8.
故存在m=2、k=8,使得b1、bm、bk成等比数列.(14分)
分析:(1)设出其首项和公差,直接利用S10=55,S20=210求出首项和公差即可求数列{an}的通项公式;
(2)先求出
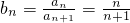 ,再代入b1、bm、bk成等比数列对应的等量关系,求出m、k之间的关系式,再利用题中k>m≥2,k,m∈N*,即可求出对应的m、k的值.
,再代入b1、bm、bk成等比数列对应的等量关系,求出m、k之间的关系式,再利用题中k>m≥2,k,m∈N*,即可求出对应的m、k的值.点评:本题第一问主要考查利用等差数列的前n项和求数列{an}的通项公式以及等比关系的确定,是对等差数列,等比数列基础知识的考查.作这一类型题目,一般是设出基本量,利用已知条件列出等量关系,再进行求解即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.