题目内容
设数列{an}的前n项和为Sn,对任意的正整数n,都有an=5Sn+1成立,记 ,
,
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)记cn=b2n-b2n-1(n∈N*),设数列{cn}的前n项和为Tn,求证:对任意正整数n都有Tn< ;
;
(Ⅲ)设数列{bn}的前n项和为Rn。已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值。
 ,
,(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)记cn=b2n-b2n-1(n∈N*),设数列{cn}的前n项和为Tn,求证:对任意正整数n都有Tn<
 ;
;(Ⅲ)设数列{bn}的前n项和为Rn。已知正实数λ满足:对任意正整数n,Rn≤λn恒成立,求λ的最小值。
解:(Ⅰ)当n=1时,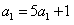 ,∴
,∴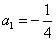 ,
,
又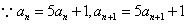 ,
,
∴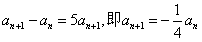 ,
,
∴数列{an}成等比数列,其首项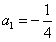 ,公比是
,公比是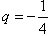 ,
,
∴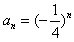 ,
,
∴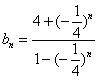 。
。
(Ⅱ)由(Ⅰ)知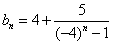 ,
,
∴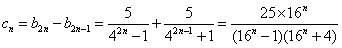
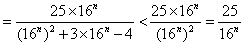 ,
,
又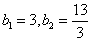 ,
,
∴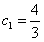 ,
,
当n=1时,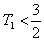 ;
;
当n≥2时,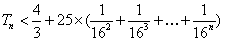
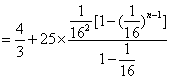
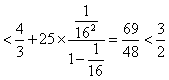 ;
;
(Ⅲ)由(Ⅰ)知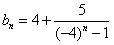 ,
,
一方面,已知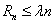 恒成立,
恒成立,
取n为大于1的奇数时,设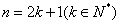 ,
,
则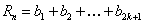
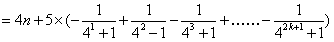
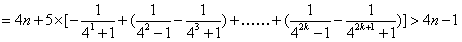 ,
,
∴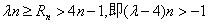 对一切大于1的奇数n恒成立,
对一切大于1的奇数n恒成立,
∴λ≥4,否则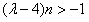 只对满足的正奇数n成立,矛盾。
只对满足的正奇数n成立,矛盾。
另一方面,当λ=4时,对一切的正整数n都有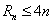 ,
,
事实上,对任意的正整数k,有
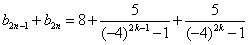
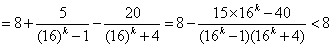 ,
,
∴当n为偶数时,设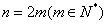 ,
,
则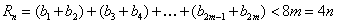 ;
;
当n为奇数时,设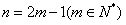 ,
,
则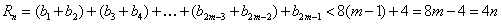 ;
;
∴对一切的正整数n,都有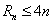 ;
;
综上所述,正实数λ的最小值为4。
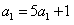 ,∴
,∴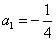 ,
,又
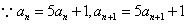 ,
,∴
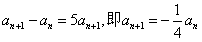 ,
,∴数列{an}成等比数列,其首项
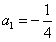 ,公比是
,公比是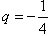 ,
, ∴
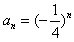 ,
,∴
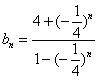 。
。(Ⅱ)由(Ⅰ)知
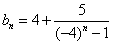 ,
,∴
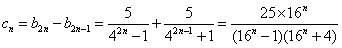
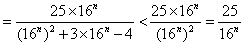 ,
,又
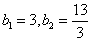 ,
,∴
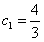 ,
,当n=1时,
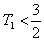 ;
;当n≥2时,
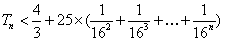
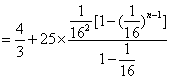
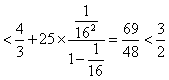 ;
;(Ⅲ)由(Ⅰ)知
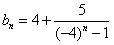 ,
,一方面,已知
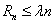 恒成立,
恒成立,取n为大于1的奇数时,设
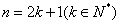 ,
,则
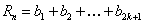
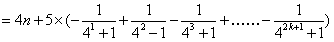
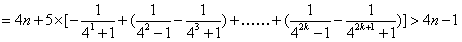 ,
,∴
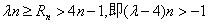 对一切大于1的奇数n恒成立,
对一切大于1的奇数n恒成立,∴λ≥4,否则
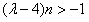 只对满足的正奇数n成立,矛盾。
只对满足的正奇数n成立,矛盾。另一方面,当λ=4时,对一切的正整数n都有
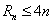 ,
,事实上,对任意的正整数k,有
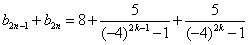
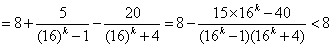 ,
,∴当n为偶数时,设
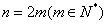 ,
,则
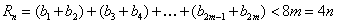 ;
;当n为奇数时,设
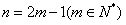 ,
,则
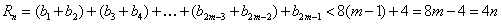 ;
;∴对一切的正整数n,都有
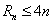 ;
;综上所述,正实数λ的最小值为4。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目