题目内容
已知函数f(x)=ex-mx的图象为曲线C,若曲线C不存在与直线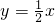 垂直的切线,则实数m的取值范围是
垂直的切线,则实数m的取值范围是
- A.

- B.

- C.m≤2
- D.m>2
C
分析:由曲线C:f(x)=ex-mx,知f′(x)=ex-m,由曲线C不存在与直线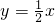 垂直的切线,知m≠2+ex>2,由此能求出结果.
垂直的切线,知m≠2+ex>2,由此能求出结果.
解答:∵曲线C:f(x)=ex-mx,
∴f′(x)=ex-m,
∵曲线C不存在与直线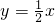 垂直的切线,
垂直的切线,
∴f′(x)=ex-m≠-2,
∴m≠2+ex>2,
观察题设中的四个选项,C最符合,
故选C.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
分析:由曲线C:f(x)=ex-mx,知f′(x)=ex-m,由曲线C不存在与直线
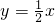 垂直的切线,知m≠2+ex>2,由此能求出结果.
垂直的切线,知m≠2+ex>2,由此能求出结果.解答:∵曲线C:f(x)=ex-mx,
∴f′(x)=ex-m,
∵曲线C不存在与直线
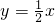 垂直的切线,
垂直的切线,∴f′(x)=ex-m≠-2,
∴m≠2+ex>2,
观察题设中的四个选项,C最符合,
故选C.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目