题目内容
已知![]() ,设
,设![]() =
=![]() (1).求
(1).求![]() 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)设关于![]() 的方程
的方程![]() =
=![]() 在
在![]() 有两个不相等的实数根,求
有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
解:(1)由f(x)=![]() ·
·![]() 得
得
f(x)=(cos![]() +sin
+sin![]() )·(cos
)·(cos![]() -sin
-sin![]() )+(-sin
)+(-sin![]() )·2cos
)·2cos![]() =cos2
=cos2![]() -sin2
-sin2![]() -2sin
-2sin![]() cos
cos![]()
=cosx-sinx=![]() cos(x+
cos(x+![]() ), ------------4分
), ------------4分
所以f(x)的最小正周期T=2π. ----------5分
又由2kπ≤x+![]() ≤π+2kπ,k∈Z,得-
≤π+2kπ,k∈Z,得-![]() +2kπ≤x≤
+2kπ≤x≤![]() +2kπ,k∈Z.
+2kπ,k∈Z.
故f(x)的单调递减区间是[-![]() +2kπ,
+2kπ,![]() +2kπ](k∈Z). -------------7分
+2kπ](k∈Z). -------------7分
(2)由f(x)=![]() 得
得![]() cos(x+
cos(x+![]() )=
)=![]() ,故cos(x+
,故cos(x+![]() )=
)=![]()
![]() -----------8分
-----------8分
又x∈![]() ,于是有x+
,于是有x+![]() ∈
∈![]() ,数形结合得[来源:Z|xx|k.Com]
,数形结合得[来源:Z|xx|k.Com]
![]()
![]()
![]() <1 -------11分
<1 -------11分
∴![]() <
<![]() ]
]
所以![]() 的取值范围是[1,
的取值范围是[1,![]() ) -----12分
) -----12分

练习册系列答案
相关题目
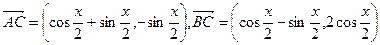 ,设
,设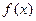 =
=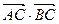 (1).求
(1).求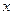 的方程
的方程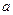 在
在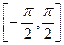 有两个不相等的实数根,求
有两个不相等的实数根,求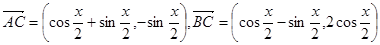 ,设
,设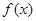 =
=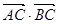 (1).求
(1).求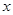 的方程
的方程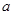 在
在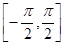 有两个不相等的实数根,求
有两个不相等的实数根,求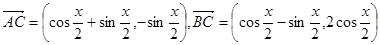 ,设
,设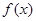 =
=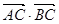 (1).求
(1).求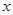 的方程
的方程 在
在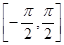 有两个不相等的实数根,求
有两个不相等的实数根,求