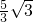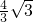Question

一动点P由正四面体ABCD的B点出发，经过△ACD的中心后到达AD中点，若AB=2，则P点行走的最短路程是（　　）

• A、

  5

  3

  3

• B、

  4

  3

  3

• C、

  3

• D、其他

Answer 1

分析：正方体表面上两点之间的最小距离问题，可以用侧面展开图解决，将正方体表面展开，求EF两点之间的距离即可．

解答：解：作出展开图，
设△ACB边AC的中点是E，△ACD的中心是G，AD中点是F，则最短路程为BE+EG+GF，
其和等于

3

+

3

3

+

3

3

=

5

3

3

．
故选A．

点评：本题考查立体几何表面距离最短问题，用到转化的思想：将空间距离转化为平面上两点间距离问题来处理，要注意体会转化思想的应用．