题目内容
(本小题满分13分)等差数列{an}中,公差d≠0,已知数列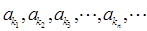 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25.
(1)求数列{kn}的通项;
(2)若a1=9,设bn=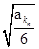 +
+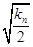 ,Sn=b12+b22+b32+…+ bn2, Tn=
,Sn=b12+b22+b32+…+ bn2, Tn= 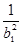 +
+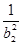 +
+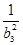 +…+
+…+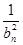 ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
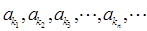 是等比数列,其中k1=1,k2=7,k3=25.
是等比数列,其中k1=1,k2=7,k3=25.(1)求数列{kn}的通项;
(2)若a1=9,设bn=
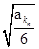 +
+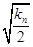 ,Sn=b12+b22+b32+…+ bn2, Tn=
,Sn=b12+b22+b32+…+ bn2, Tn= 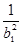 +
+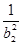 +
+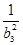 +…+
+…+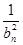 ,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。
,试判断数列{Sn+Tn}前100项中有多少项是能被4整除的整数。(1) (2)
(2) 前
前 项中有100项是能被4整除的整数
项中有100项是能被4整除的整数
 (2)
(2) 前
前 项中有100项是能被4整除的整数
项中有100项是能被4整除的整数(1)利用等差和等比数列的性质得出关于kn的式子,进一步求出通项;(2)先求出bn,进一步求出 的通项公式,再利用二项式知识解决整除问题
的通项公式,再利用二项式知识解决整除问题
解:(1)由 得到:
得到: ,所以:
,所以: ,
,
因为公差 ,得:
,得: ,即
,即 ,
,
所以等比数列 的公比是
的公比是 ,……………………4分
,……………………4分
得到: ,即
,即 .…………………………………………6分
.…………………………………………6分
(2) ,所以:
,所以: ,…………………7分
,…………………7分
则: -2=
-2= ,
,
所以: =
= ………………………………………9分
………………………………………9分
当 为偶数时:
为偶数时: ,能被4整除,
,能被4整除, 也能被4整除,
也能被4整除,
所以 能被4整除.………………………………………………………………11分
能被4整除.………………………………………………………………11分
当 为奇数时,
为奇数时, ,
,
 能被4整除,
能被4整除, 也能被4整除,
也能被4整除,
所以 能被4整除.………………………………………………………………12分
能被4整除.………………………………………………………………12分
所以数列 前
前 项中有100项是能被4整除的整数.…………………13分
项中有100项是能被4整除的整数.…………………13分
 的通项公式,再利用二项式知识解决整除问题
的通项公式,再利用二项式知识解决整除问题解:(1)由
 得到:
得到: ,所以:
,所以: ,
,因为公差
 ,得:
,得: ,即
,即 ,
,所以等比数列
 的公比是
的公比是 ,……………………4分
,……………………4分得到:
 ,即
,即 .…………………………………………6分
.…………………………………………6分(2)
 ,所以:
,所以: ,…………………7分
,…………………7分则:
 -2=
-2= ,
,所以:
 =
= ………………………………………9分
………………………………………9分当
 为偶数时:
为偶数时: ,能被4整除,
,能被4整除, 也能被4整除,
也能被4整除,所以
 能被4整除.………………………………………………………………11分
能被4整除.………………………………………………………………11分当
 为奇数时,
为奇数时, ,
, 能被4整除,
能被4整除, 也能被4整除,
也能被4整除,所以
 能被4整除.………………………………………………………………12分
能被4整除.………………………………………………………………12分所以数列
 前
前 项中有100项是能被4整除的整数.…………………13分
项中有100项是能被4整除的整数.…………………13分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
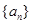 中,
中,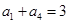 ,
,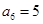 .
.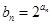 ,求数列
,求数列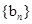 的前10项的和
的前10项的和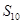 .
.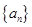 是首项为1,公比为2的等比数列,数列
是首项为1,公比为2的等比数列,数列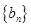 的前
的前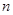 项和
项和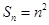 .
.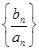 的前
的前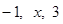 ,则它的第五项为 .
,则它的第五项为 . 的前5项和为105,且
的前5项和为105,且 .
. ,将数列
,将数列 的项的个数记为
的项的个数记为 .求数列
.求数列 的前m项和
的前m项和 .
.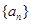 为等差数列,若
为等差数列,若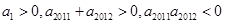 ,则使前
,则使前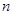 项
项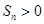 的最大自然数
的最大自然数 项的和
项的和 等于
等于


 ( )
( ) ,其中
,其中 ,则
,则 的值为( )
的值为( )