题目内容
如图,在半径为 、圆心角为60°的扇形的
、圆心角为60°的扇形的 弧上任取一点
弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在 上,设矩形
上,设矩形 的面积为
的面积为 .
.
(1)按下列要求写出函数关系式:
①设 ,将
,将 表示成
表示成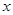 的函数关系式;
的函数关系式;
②设 ,将
,将 表示成
表示成 的函数关系式.
的函数关系式.
(2)请你选用(1)中的一个函数关系式,求 的最大值.
的最大值.
(1) ① (
( ),②
),② (
( );(2) 选②,当
);(2) 选②,当 时,y取得最大值为
时,y取得最大值为 .
.
解析试题分析:(1) ①设 ,则
,则 ,三角形中有
,三角形中有 ,又
,又 ,则
,则 ,又
,又 ,可得表达式, ②当
,可得表达式, ②当 时,
时, ,三角形中同样有
,三角形中同样有 ,
, ,
, ,由
,由 得表达式;(2) 将
得表达式;(2) 将 化为
化为 ,可得最大值
,可得最大值 .
.
试题解析:解:(1) ① 因为 ,所以
,所以 ,又
,又 ,
,
所以 3分
3分
故 (
( ) 5分
) 5分
② 当 时,
时,  ,则
,则 ,又
,又 ,
,
所以 8分
8分
故 (
( ) 10分
) 10分
(2)由②得 =
= 13分
13分
故当 时,y取得最大值为
时,y取得最大值为 16分
16分
考点:1.倍角公式;2.正弦函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的值是 。
的值是 。 ,且
,且 .
. 的值; (2)求
的值; (2)求 的值.
的值. .
. 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,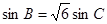
 的值;
的值; 的值.
的值.
 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;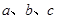 满足
满足 ,且边
,且边 所对的角为
所对的角为 ,试求
,试求 ,且
,且 .
. 的值;
的值;  的值.
的值. 
 的最小正周期;
的最小正周期; ,
, 的值.
的值. ,则
,则 等于__________
等于__________