题目内容
已知P是圆F1:(x+1)2+y2=16上的动点,点F2(1,0),线段PF2的垂直平分线l与半径F1P交于点Q.
(I)当点P在圆上运动时,求点Q的轨迹C的方程.
(II)已知点M(1,
),A、B在(1)中所求的曲线C上,且
+
=λ
(λ∈R,O是坐标原点),
(i)求直线AB的斜率;
(ii)求证:当△MAB的面积取得最大值时,O是△MAB的重心.
(I)当点P在圆上运动时,求点Q的轨迹C的方程.
(II)已知点M(1,
| 3 |
| 2 |
| MA |
| MB |
| OM |
(i)求直线AB的斜率;
(ii)求证:当△MAB的面积取得最大值时,O是△MAB的重心.
分析:(I)根据圆M的标准方程得到点M坐标(-1,0),圆的半径R=4,再由线段中垂线定理,可得出点Q的轨迹C是椭圆,从而可得出点G的轨迹C对应的椭圆的标准方程;
(II)(i)设A(x1,y1),B(x2,y2),由
+
=λ
得
,再利用点差法,即可求得直线AB的斜率;
(ii)设AB的直线方程为y=-
x+t,代入椭圆C的方程,求出|AB|及P到直线AB的距离,从而可得△MAB的面积,利用基本不等式求最值,即可证得结论.
(II)(i)设A(x1,y1),B(x2,y2),由
| MA |
| MB |
| OM |
|
(ii)设AB的直线方程为y=-
| 1 |
| 2 |
解答:(I)解:根据题设有|QP|=|QF2|,|F1P|=4
∴|QF1|+|QF2|=|QF1|+|QP|=|F1P|=4
∵|F1F2|=2<4
∴根据椭圆的定义可知,Q的轨迹为以F1(-1,0),F2(1,0)为焦点中心在原点半长轴为2,半焦距为1,半短轴为
的椭圆,其方程为
+
=1
(II)(i)解:设A(x1,y1),B(x2,y2),由
+
=λ
得
1-x1+1-x2=λ,
-y1+
-y2=
λ
∴
由
+
=1,
+
=1,
两式相减可得
+
=0
直线AB的斜率为
=-
×
=-
;
(ii)证明:设AB的直线方程为y=-
x+t,代入椭圆C的方程,整理得x2-tx+t2-3=0
∴△=3(4-t2)>0,|AB|=
×
=
∵P到直线AB的距离d=
∴△MAB的面积为S=
|2-t|
(-2<t<2)
∴S2=
(2-t)3(6+3t)≤
×[
]4=
∴S≤
,当且仅当2-t=6+3t,即t=-1时取等号
∴当t=-1时,三角形的面积S取得最大值
,
根据韦达定理得x1+x2=t=-1,∴x1+x2=2+λ=-1,∴λ=-3
∴
=0,
=0
故O是△MAB的重心.
∴|QF1|+|QF2|=|QF1|+|QP|=|F1P|=4
∵|F1F2|=2<4
∴根据椭圆的定义可知,Q的轨迹为以F1(-1,0),F2(1,0)为焦点中心在原点半长轴为2,半焦距为1,半短轴为
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
(II)(i)解:设A(x1,y1),B(x2,y2),由
| MA |
| MB |
| OM |
1-x1+1-x2=λ,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴
|
由
| x12 |
| 4 |
| y12 |
| 3 |
| x22 |
| 4 |
| y22 |
| 3 |
两式相减可得
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
直线AB的斜率为
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| x1+x2 |
| y1+y2 |
| 1 |
| 2 |
(ii)证明:设AB的直线方程为y=-
| 1 |
| 2 |
∴△=3(4-t2)>0,|AB|=
1+
|
| 3(4-t2) |
| ||
| 2 |
| 3(4-t2) |
∵P到直线AB的距离d=
| |4-2t| | ||
|
∴△MAB的面积为S=
| ||
| 2 |
| 4-t2 |
∴S2=
| 1 |
| 4 |
| 1 |
| 4 |
| (2-t)+(2-t)+(2-t)+(6+3t) |
| 4 |
| 81 |
| 4 |
∴S≤
| 9 |
| 2 |
∴当t=-1时,三角形的面积S取得最大值
| 9 |
| 2 |
根据韦达定理得x1+x2=t=-1,∴x1+x2=2+λ=-1,∴λ=-3
∴
| x1+x2+1 |
| 3 |
y1+y2+
| ||
| 3 |
故O是△MAB的重心.
点评:本题借助一个动点的轨迹,得到椭圆的第一定义,进而求出其轨迹方程,考查向量知识的运用,考查三角形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),A、B在(1)中所求的曲线C上,且
),A、B在(1)中所求的曲线C上,且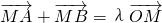 (λ∈R,O是坐标原点),
(λ∈R,O是坐标原点), ),A、B在(1)中所求的曲线C上,且
),A、B在(1)中所求的曲线C上,且 (λ∈R,O是坐标原点),
(λ∈R,O是坐标原点), ),A、B在(1)中所求的曲线C上,且
),A、B在(1)中所求的曲线C上,且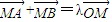 (λ∈R,O是坐标原点),
(λ∈R,O是坐标原点),