题目内容
函数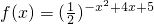 的单调递增区间为________.
的单调递增区间为________.
[2,+∞)
分析:由题意,本题是一个复合函数,外层函数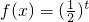 是一个减函数,故复合函数的单调递增区间即是内层函数的单调递减区间,由此解出内层函数的单调递减区间即可得到答案
是一个减函数,故复合函数的单调递增区间即是内层函数的单调递减区间,由此解出内层函数的单调递减区间即可得到答案
解答:函数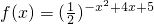 由函数
由函数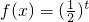 与函数t=-x2+4x+5复合而成
与函数t=-x2+4x+5复合而成
函数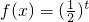 是减函数,由复合函数的单调性知,函数
是减函数,由复合函数的单调性知,函数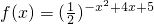 的单调递增区间即是内层函数t=-x2+4x+5的单调递减区间
的单调递增区间即是内层函数t=-x2+4x+5的单调递减区间
由于t=-x2+4x+5的单调递减区间是[2,+∞)
故答案为[2,+∞)
点评:本题考查复合函数的单调性,解题的关键是熟练掌握复合函数的单调性的判断规则,由利用它判断出判断出函数的递增区间即是内层函数的递减区间,本题考查了推理判断能力及转化的思想,属于对单调性考查的基本题型.
分析:由题意,本题是一个复合函数,外层函数
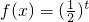 是一个减函数,故复合函数的单调递增区间即是内层函数的单调递减区间,由此解出内层函数的单调递减区间即可得到答案
是一个减函数,故复合函数的单调递增区间即是内层函数的单调递减区间,由此解出内层函数的单调递减区间即可得到答案解答:函数
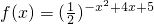 由函数
由函数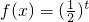 与函数t=-x2+4x+5复合而成
与函数t=-x2+4x+5复合而成函数
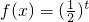 是减函数,由复合函数的单调性知,函数
是减函数,由复合函数的单调性知,函数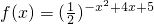 的单调递增区间即是内层函数t=-x2+4x+5的单调递减区间
的单调递增区间即是内层函数t=-x2+4x+5的单调递减区间由于t=-x2+4x+5的单调递减区间是[2,+∞)
故答案为[2,+∞)
点评:本题考查复合函数的单调性,解题的关键是熟练掌握复合函数的单调性的判断规则,由利用它判断出判断出函数的递增区间即是内层函数的递减区间,本题考查了推理判断能力及转化的思想,属于对单调性考查的基本题型.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的单调递增区间为________________
的单调递增区间为________________ 的单调递增区间为
。
的单调递增区间为
。