题目内容
 已知函数f(x)=sin(ωx+φ)(ω>0,
已知函数f(x)=sin(ωx+φ)(ω>0, )的部分图象如图所示,则ω=________;函数f(x)在区间
)的部分图象如图所示,则ω=________;函数f(x)在区间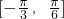 上的最大值为________.
上的最大值为________.
2 
分析:根据所给的图象看出函数的四分之一个周期,求出函数的周期,根据周期的公式做出ω,根据图象上的点代入解析式,即由( ,1)确定φ,确定函数的解析式以后,得到闭区间上的最大值.
,1)确定φ,确定函数的解析式以后,得到闭区间上的最大值.
解答:由图象可知: ,得T=π,
,得T=π,
∵
∴ω=2;
∴函数的解析式是y=sin(2x+φ)
∵( ,1)在图象上,有1=sin(2×
,1)在图象上,有1=sin(2× +φ)
+φ)
所以2× +φ=
+φ= ,φ=-
,φ=- .
.
∴函数的解析式是y=sin(2x- )
)
当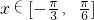 时,2x
时,2x ,2x-
,2x-

∴sin(2x- )
)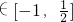
∴函数的最大值是 ,
,
故答案为:2;
点评:本题考查y=Asin(ωx+φ)中参数的意义,本题解题的关键是由y=Asin(ωx+φ)的部分图象确定其解析式,特别是其中初相的求法,本题考查视图能力,要求能够从图形中看出要用的数据,本题是一个中档题目.

分析:根据所给的图象看出函数的四分之一个周期,求出函数的周期,根据周期的公式做出ω,根据图象上的点代入解析式,即由(
 ,1)确定φ,确定函数的解析式以后,得到闭区间上的最大值.
,1)确定φ,确定函数的解析式以后,得到闭区间上的最大值.解答:由图象可知:
 ,得T=π,
,得T=π,∵

∴ω=2;
∴函数的解析式是y=sin(2x+φ)
∵(
 ,1)在图象上,有1=sin(2×
,1)在图象上,有1=sin(2× +φ)
+φ)所以2×
 +φ=
+φ= ,φ=-
,φ=- .
.∴函数的解析式是y=sin(2x-
 )
)当
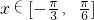 时,2x
时,2x ,2x-
,2x-

∴sin(2x-
 )
)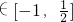
∴函数的最大值是
 ,
,故答案为:2;

点评:本题考查y=Asin(ωx+φ)中参数的意义,本题解题的关键是由y=Asin(ωx+φ)的部分图象确定其解析式,特别是其中初相的求法,本题考查视图能力,要求能够从图形中看出要用的数据,本题是一个中档题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
