题目内容
8. 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 7+$\sqrt{5}$ | B. | 7+2$\sqrt{5}$ | C. | 4+2$\sqrt{2}$ | D. | 4+$\sqrt{5}$ |
分析 几何体为从正方体中切出来的三棱锥,利用正方体模型计算三棱锥的各边,再计算面积.
解答 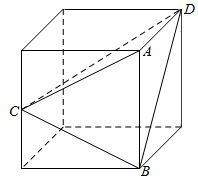 解:由三视图可知几何体为从边长为2正方体中切出来的三棱锥A-BCD,如图所示.其中C为正方体棱的中点,
解:由三视图可知几何体为从边长为2正方体中切出来的三棱锥A-BCD,如图所示.其中C为正方体棱的中点,
∴S△ABC=$\frac{1}{2}×2×2$=2,SABD=$\frac{1}{2}×2×2$=2,
∵AC=BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,∴S△ACD=$\frac{1}{2}×2×\sqrt{5}$=$\sqrt{5}$.
∵CD=$\sqrt{A{D}^{2}+A{C}^{2}}$=3,BD=2$\sqrt{2}$,∴cos∠CBD=$\frac{B{C}^{2}+B{D}^{2}-C{D}^{2}}{2BC•BD}$=$\frac{\sqrt{10}}{10}$.
∴sin∠CBD=$\frac{3\sqrt{10}}{10}$.
∴S△BCD=$\frac{1}{2}×\sqrt{5}×2\sqrt{2}×\frac{3\sqrt{10}}{10}$=3.
∴几何体的表面积S=2+2+$\sqrt{5}$+3=7+$\sqrt{5}$.
故选A.
点评 本题考查了不规则放置的几何体的三视图及面积计算,作出直观图是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
3.若f(x)在[a,b]上连续,则下列说法正确的是( )
| A. | f(x)在[a,b]上可导 | |
| B. | ${∫}_{a}^{x}$f(t)dt为f(x)在[a,b]上的一个原函数: | |
| C. | ${∫}_{x}^{b}$f(t)dt为f(x)在[a,b]上的一个原函数 | |
| D. | f(x)在[a,b]上至少有一个零点 |