题目内容
设- ≤x≤
≤x≤ ,函数y=log2(1+sinx)+log2(1-sinx)的最大值是________,最小值是________.
,函数y=log2(1+sinx)+log2(1-sinx)的最大值是________,最小值是________.
0 -1
分析:先根据对数的运算性质将函数y化简,再由x的范围可求函数y的最值.
解答:∵y=log2(1+sinx)+log2(1-sinx)
=log2[(1+sinx)(1-sinx)]=log2(1-sin2x)=log2cosx2x=2log2cosx
∵- ≤x≤
≤x≤ ∴
∴ ≤cosx≤1∴-1≤2log2cosx≤0
≤cosx≤1∴-1≤2log2cosx≤0
故答案为:0,-1
点评:本题主要考查对数的运算性质.属基础题.
分析:先根据对数的运算性质将函数y化简,再由x的范围可求函数y的最值.
解答:∵y=log2(1+sinx)+log2(1-sinx)
=log2[(1+sinx)(1-sinx)]=log2(1-sin2x)=log2cosx2x=2log2cosx
∵-
 ≤x≤
≤x≤ ∴
∴ ≤cosx≤1∴-1≤2log2cosx≤0
≤cosx≤1∴-1≤2log2cosx≤0故答案为:0,-1
点评:本题主要考查对数的运算性质.属基础题.

练习册系列答案
相关题目
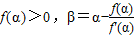 ,试探究实数α、β、x的大小关系.
,试探究实数α、β、x的大小关系.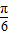 ≤x≤
≤x≤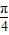 ,函数y=log2(1+sinx)+log2(1-sinx)的最大值是 ,最小值是 .
,函数y=log2(1+sinx)+log2(1-sinx)的最大值是 ,最小值是 .