题目内容
已知实数x,y满足不等关系: ,则目标函数z=3x+9y的最小值是
,则目标函数z=3x+9y的最小值是
- A.22
- B.36
- C.72
- D.12
A
分析:画出平面区域,根据目标函数的特点确定其取得最小值的点,即可求出其最小值.
解答: 解:不等式组:
解:不等式组: ,所表示的平面区域,如图所示.
,所表示的平面区域,如图所示.
由 得B(
得B( ,
, )
)
显然目标函数在点B( ,
, )处取得最小值3×
)处取得最小值3× +9×
+9× =22.
=22.
故选A.
点评:本题考查不等式组所表示的平面区域和简单的线性规划问题.在线性规划问题中目标函数取得最值的点一定是区域的顶点和边界,在边界上的值也等于在这个边界上的顶点的值,故在解答选择题或者填空题时,只要能把区域的顶点求出,直接把顶点坐标代入进行检验即可.
分析:画出平面区域,根据目标函数的特点确定其取得最小值的点,即可求出其最小值.
解答:
 解:不等式组:
解:不等式组: ,所表示的平面区域,如图所示.
,所表示的平面区域,如图所示.由
 得B(
得B( ,
, )
)显然目标函数在点B(
 ,
, )处取得最小值3×
)处取得最小值3× +9×
+9× =22.
=22.故选A.
点评:本题考查不等式组所表示的平面区域和简单的线性规划问题.在线性规划问题中目标函数取得最值的点一定是区域的顶点和边界,在边界上的值也等于在这个边界上的顶点的值,故在解答选择题或者填空题时,只要能把区域的顶点求出,直接把顶点坐标代入进行检验即可.

练习册系列答案
相关题目
 ,则目标函数z=x-y的最大值等于( )
,则目标函数z=x-y的最大值等于( )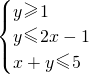 ,则目标函数z=x-y的最大值等于________.
,则目标函数z=x-y的最大值等于________. ,则目标函数z=x-y的最大值等于 .
,则目标函数z=x-y的最大值等于 .