题目内容
已知角α的顶点与直角坐标系原点O重合,始边与x轴的非负半轴重合,终边与单位圆交于点P,且α∈[0,π)设点M的坐标是 ,求使得函数
,求使得函数 的恰有两个零点的实数k的取值范围 .
的恰有两个零点的实数k的取值范围 .
【答案】分析:利用向量的数量积和两角和的正弦公式可得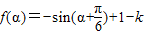 ,再根据正弦函数的图象和单调性即可得出.
,再根据正弦函数的图象和单调性即可得出.
解答:解:f(α)=(cosα,sinα)•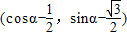 -k=
-k=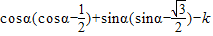 =
=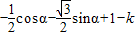 =
=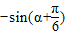 +1-k.
+1-k.
化为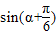 =1-k,
=1-k,
∵α∈[0,π),∴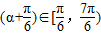 ,∴
,∴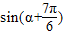 ∈
∈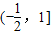 ,
,
要使得函数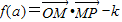 的恰有两个零点,则
的恰有两个零点,则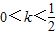 .
.
故答案为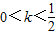 .
.
点评:熟练掌握向量的数量积运算、两角和的正弦公式及其三角函数的图象与性质等是解题的关键.
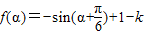 ,再根据正弦函数的图象和单调性即可得出.
,再根据正弦函数的图象和单调性即可得出.解答:解:f(α)=(cosα,sinα)•
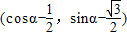 -k=
-k=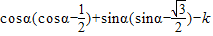 =
=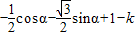 =
=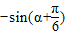 +1-k.
+1-k.化为
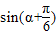 =1-k,
=1-k,∵α∈[0,π),∴
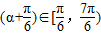 ,∴
,∴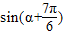 ∈
∈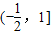 ,
,要使得函数
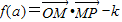 的恰有两个零点,则
的恰有两个零点,则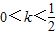 .
.故答案为
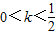 .
.点评:熟练掌握向量的数量积运算、两角和的正弦公式及其三角函数的图象与性质等是解题的关键.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
已知正△ABC的顶点A在平面α上,顶点B,C在平面α的同一侧,D为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的三角形,则直线AD与平面α所成角的正弦值的范围是( )
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、(
|