题目内容
已知等差数列{bn}中,d=-3,b7=10,(1)求b1.
(2)这个数列是递增还是递减?证明你的结论.
解:(1)∵数列{bn}是等差数列,
∴通项bn=b1+(n-1)d.
由d=-3代入得bn=b1-3(n-1),
∴b7=b1-3(7-1)=b1-18=10,
∴b1=28.
(2)根据题意和(1)得
bn=b1+(n-1)d=28-3(n-1)=-3n+31
这是关于n的一次函数,一次项系数为负值.
∴数列{bn}单调递减.
证明:bn+1-bn=-3(n+1)+31-[-3n+31]=-3<0,
∴bn+1<bn.
∴数列{bn}单调递减.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
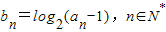 ,且已知a1=3,a3=9.
,且已知a1=3,a3=9. 为常数,则称数列{an}为“科比数列”.
为常数,则称数列{an}为“科比数列”.