Question

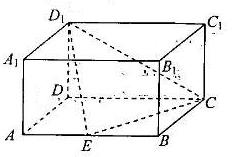如图，在长方体ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB=2，点E为棱AB的中点．
（1）证明：D₁⊥A₁D；
（2）求二面角D₁-EC-D的大小；
（3）求点D到平面D₁EC的距离．

Answer 1

分析：（1）连接A₁D，AD₁，根据长方体的几何特征，我们易得AD₁是D₁E在平面AD₁内的射影，由AD=A₁A，可得四边形A₁DD₁A为正方形，进而根据三垂线定理可得D₁E⊥A₁D；
（2）连接DE，根据等腰直角三角形的性质，及线面垂直的判定和性质，可得DE⊥EC，D₁E⊥EC，进而由∠D₁ED即为二面角D₁-EC-D的平面角，解三角形D₁ED即可得到二面角D₁-EC-D的大小；
（3）过点D作DF⊥D₁E于F，结合（2）的结论，可证得DF⊥面D₁EC，即DF为点D到平面D₁EC的距离，根据等面积法，我们易解三角形D₁ED得到DF长．

解答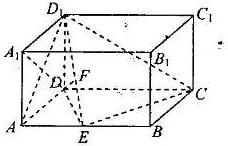：证明：（1）连接A₁D，AD₁，在长方体中，AE⊥平面AD₁
∴AD₁是D₁E在平面AD₁内的投影，
∵AD=A₁A
∴四边形A₁DD₁A为正方形，
∴AD₁⊥A₁D，
由三垂线定理：
D₁E⊥A₁D，…（4分）
解：（2）连接DE，
∵E为AB的中点，
∴AD=AE，EB=BC
∴∠AED=∠BEC=45°
∴DE⊥EC
∴DD₁⊥平面ABCD
∴D₁E⊥EC
故∠D₁ED即为二面角D₁-EC-D的平面角
在△D₁ED中，DD₁=1，DE=

2

∴∴tan∠D1ED=

DD1

DE

=

2

2

故二面角D₁-EC-D的大小为arctan

2

2

…..（8分）
（3）过点D作DF⊥D₁E于F
由（2）可得EC⊥面D₁DE，有EC?面D₁EC
∴面D₁EC⊥面D₁DE
∴DF⊥面D₁EC
故DF为点D到平面D₁EC的距离…（10分）
∵D₁E²=DE²+DD₁²
∴D₁E=

3

，
DF=

DD1•DE

D1E

=

6

3

故点D到平面D₁EC的距离为

6

3

…（12分）

点评：本题考查的知识点是二面角的平面角及求法，直线与平面垂直的性质，点到平面之间的距离，其中（1）的关键是使用三垂线定理，（2）的关键是证得∠D₁ED即为二面角D₁-EC-D的平面角，（3）的关键是证得DF为点D到平面D₁EC的距离．