题目内容
已知函数f(x)=sin2ωx+ sinωxsin(ωx+
sinωxsin(ωx+ )-
)- (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值;
(2)求f(x)的最大值及取最大值时x的取值集合;
(3)若方程f(x)=k-1在[0,π]内有两个相异的实数根,求实数k的取值范围.
解:(1)∵f(x)=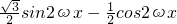 =
=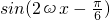 的最小正周期为π,∴ω=1;
的最小正周期为π,∴ω=1;
(2)当2x- =
=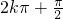 ,x
,x (k∈Z),f(x)max=1;
(k∈Z),f(x)max=1;
(3)∵x∈[0,π],∴ ,
,
∵方程f(x)=k-1在[0,π]内有两个相异的实数根,∴ ,
,
解得, .
.
分析:(1)利用三角函数的诱导公式与辅助角公式可将函数化为f(x)=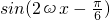 ,利用正弦函数的周期公式可求ω;
,利用正弦函数的周期公式可求ω;
(2)由f(x)=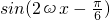 ,可求f(x)的最大值及取最大值时x的取值集合;
,可求f(x)的最大值及取最大值时x的取值集合;
(3)作出y=sinx, 的图象,作出y=k-1 的图象,数形结合可求得k的范围.
的图象,作出y=k-1 的图象,数形结合可求得k的范围.
点评:本题考查三角函数的最值,重点考查三角函数中的辅助角公式的应用及数形结合的数学思想,属于中档题.
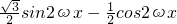 =
=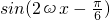 的最小正周期为π,∴ω=1;
的最小正周期为π,∴ω=1;(2)当2x-
 =
=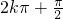 ,x
,x (k∈Z),f(x)max=1;
(k∈Z),f(x)max=1;(3)∵x∈[0,π],∴
 ,
,∵方程f(x)=k-1在[0,π]内有两个相异的实数根,∴
 ,
,解得,
 .
.分析:(1)利用三角函数的诱导公式与辅助角公式可将函数化为f(x)=
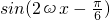 ,利用正弦函数的周期公式可求ω;
,利用正弦函数的周期公式可求ω;(2)由f(x)=
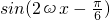 ,可求f(x)的最大值及取最大值时x的取值集合;
,可求f(x)的最大值及取最大值时x的取值集合;(3)作出y=sinx,
 的图象,作出y=k-1 的图象,数形结合可求得k的范围.
的图象,作出y=k-1 的图象,数形结合可求得k的范围.点评:本题考查三角函数的最值,重点考查三角函数中的辅助角公式的应用及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
