题目内容
在△ABC中,AB= ,BC=1,cosC=
,BC=1,cosC= .(1)求sinA的值;(2)求AC.
.(1)求sinA的值;(2)求AC.
解:(1)在△ABC中,因为 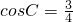 ,
,
所以 ,
,
又由正弦定理: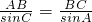 可得:
可得: .
.
(2)由余弦定理:AB2=AC2+BC2-2AC•BC•cosC得: ,
,
所以整理可得: ,
,
解得b=2或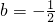 (舍去),
(舍去),
所以AC=2.
分析:(1)利用同角三角函数基本关系,根据cosC,求得sinC,进而利用正弦定理求得sinA.
(2)在三角形中根据已知的边与角,进而判断出能够利用余弦定理求得b.
点评:本题主要考查了正弦定理的应用,一元二次方程的解法,解题过程要灵活运用余弦定理,属于基础题.
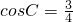 ,
,所以
 ,
,又由正弦定理:
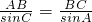 可得:
可得: .
.(2)由余弦定理:AB2=AC2+BC2-2AC•BC•cosC得:
 ,
,所以整理可得:
 ,
,解得b=2或
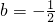 (舍去),
(舍去),所以AC=2.
分析:(1)利用同角三角函数基本关系,根据cosC,求得sinC,进而利用正弦定理求得sinA.
(2)在三角形中根据已知的边与角,进而判断出能够利用余弦定理求得b.
点评:本题主要考查了正弦定理的应用,一元二次方程的解法,解题过程要灵活运用余弦定理,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目