题目内容
4.如果θ是第二象限的角,求证sin(cosθ)•cos(sinθ)<0.分析 由θ是第二象限的角,先判断出cosθ和sinθ的取值范围,从而判断出sin(cosθ),cos(sinθ)的符号,由此能证明sin(cosθ)•cos(sinθ)<0.
解答 证明:∵θ是第二象限的角,
∴-1<cosθ<0,0<sinθ<1,
∴sin(cosθ)<0,cos(sinθ)>0,
∴sin(cosθ)•cos(sinθ)<0.
点评 本题考查三角函数值乘积小于0的证明,是基础题,解题时要认真审题,注意三角函数值在不同象限的符号的合理运用.

练习册系列答案
相关题目
8.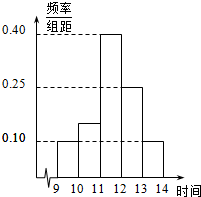 某商场在一日促销活动中,归该日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知11时至12时的销售额为10万元,则10时到11时的销售额为(单位:万元)( )
某商场在一日促销活动中,归该日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知11时至12时的销售额为10万元,则10时到11时的销售额为(单位:万元)( )
 某商场在一日促销活动中,归该日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知11时至12时的销售额为10万元,则10时到11时的销售额为(单位:万元)( )
某商场在一日促销活动中,归该日9时到14时的销售额进行统计,其频率分布直方图如图所示,已知11时至12时的销售额为10万元,则10时到11时的销售额为(单位:万元)( )| A. | 2.5 | B. | 2.75 | C. | 3.25 | D. | 3.75 |