Question

（2013•唐山一模）三棱柱ABC-A_lB₁C₁的底面是正三角形，侧棱垂直于底面，所有棱长都相等，则异面直线AB₁与BC所成角的余弦值为（　　）

• A．

  6

  4

• B．

  1

  4

• C．

  3

  4

• D．

  2

  4

Answer 1

分析：根据异面直线所成角的定义判定异面直线所成的角，再在三角形中求解即可．

解答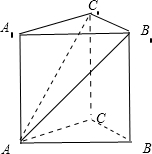：解：连接AC₁，设棱长为1，∵B₁C₁∥BC，
∴∠AB₁C₁为异面直线AB₁ 与BC所成的角，
在△AB₁C₁中，AB₁=AC₁=

2

，B₁C₁=1，
 cos∠AB₁C₁=

2+1-2

2×1× 2

=

2

4

，
故选D

点评：本题考查异面直线及其所成的角．