题目内容
设a∈R,函数f(x)=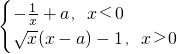
(Ⅰ)当a=2时,试确定函数f(x)的单调区间;
(Ⅱ)若对任何x∈R,且x≠0,都有f(x)>x-1,求a的取值范围.
解:(Ⅰ)当x<0时,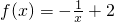 ,
,
因为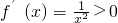 ,所以f(x)在(-∞,0)上为增函数;
,所以f(x)在(-∞,0)上为增函数;
当x>0时,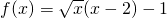 ,
, ,由f′(x)>0,解得
,由f′(x)>0,解得 ,由f′(x)<0,解得
,由f′(x)<0,解得 ,
,
所以f(x)在 上为增函数,在
上为增函数,在 上为减函数.
上为减函数.
综上,f(x)增区间为(-∞,0)和 ,减区间为
,减区间为 .
.
(Ⅱ)当x<0时,由f(x)>x-1,得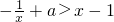 ,即
,即 ,
,
设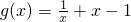 ,
,
所以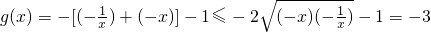 (当且仅当x=-1时取等号),
(当且仅当x=-1时取等号),
所以当x=-1时,g(x)有最大值-3,
因为对任何x<0,不等式 恒成立,所以a>-3;
恒成立,所以a>-3;
当x>0时,由f(x)>x-1,得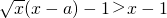 ,即
,即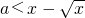 ,
,
设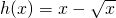 ,则
,则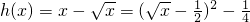 ,
,
所以当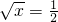 ,即
,即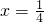 时,h(x)有最小值
时,h(x)有最小值 ,
,
因为对任何x>0,不等式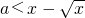 恒成立,所以
恒成立,所以 .
.
综上,实数a的取值范围为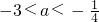 .
.
分析:(1)a=2时,当x<0时,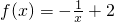 ,当x>0时,
,当x>0时,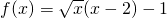 ,可用导数判单调性;
,可用导数判单调性;
(2)当x<0时,f(x)>x-1?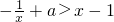 ?
? ,转化为求
,转化为求 的最大值问题
的最大值问题
当x>0时,f(x)>x-1?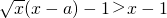 ,即
,即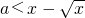 ,转化为求
,转化为求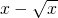 的最小值,可用导数求解.
的最小值,可用导数求解.
点评:本题考查分段函数的单调性判断、已知不等式恒成立求参数范围问题,综合性强,难度较大.
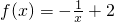 ,
,因为
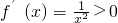 ,所以f(x)在(-∞,0)上为增函数;
,所以f(x)在(-∞,0)上为增函数;当x>0时,
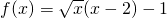 ,
, ,由f′(x)>0,解得
,由f′(x)>0,解得 ,由f′(x)<0,解得
,由f′(x)<0,解得 ,
,所以f(x)在
 上为增函数,在
上为增函数,在 上为减函数.
上为减函数.综上,f(x)增区间为(-∞,0)和
 ,减区间为
,减区间为 .
.(Ⅱ)当x<0时,由f(x)>x-1,得
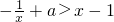 ,即
,即 ,
,设
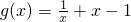 ,
,所以
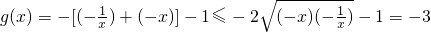 (当且仅当x=-1时取等号),
(当且仅当x=-1时取等号),所以当x=-1时,g(x)有最大值-3,
因为对任何x<0,不等式
 恒成立,所以a>-3;
恒成立,所以a>-3;当x>0时,由f(x)>x-1,得
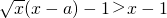 ,即
,即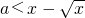 ,
,设
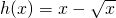 ,则
,则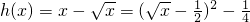 ,
,所以当
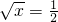 ,即
,即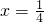 时,h(x)有最小值
时,h(x)有最小值 ,
,因为对任何x>0,不等式
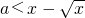 恒成立,所以
恒成立,所以 .
.综上,实数a的取值范围为
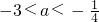 .
.分析:(1)a=2时,当x<0时,
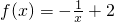 ,当x>0时,
,当x>0时,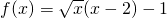 ,可用导数判单调性;
,可用导数判单调性;(2)当x<0时,f(x)>x-1?
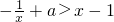 ?
? ,转化为求
,转化为求 的最大值问题
的最大值问题当x>0时,f(x)>x-1?
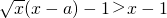 ,即
,即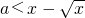 ,转化为求
,转化为求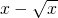 的最小值,可用导数求解.
的最小值,可用导数求解.点评:本题考查分段函数的单调性判断、已知不等式恒成立求参数范围问题,综合性强,难度较大.

练习册系列答案
相关题目
设a∈R,函数f(x)=ex-ae-x的导函数为f′(x),且f′(x)是奇函数,则a=( )
| A、0 | B、1 | C、2 | D、-1 |