题目内容
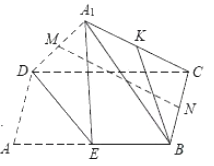
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,点
折起,点![]() 折至
折至![]() 处(
处(![]() 与
与![]() 不重合),若
不重合),若![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则在
的中点,则在![]() 折起过程中( )
折起过程中( )
A.![]() 可以与
可以与![]() 垂直
垂直
B.不能同时做到![]() 平面
平面![]() 且
且![]() 平面
平面![]()
C.当![]() 时,
时,![]() 平面
平面![]()
D.直线![]() 、
、![]() 与平面
与平面![]() 所成角分别为
所成角分别为![]() 、
、![]() ,
,![]() 、
、![]() 能够同时取得最大值
能够同时取得最大值
【答案】D
【解析】
逐一分析各选项的正误,从而可得出结论.
对于A,连接![]() ,假设
,假设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
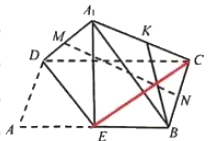
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
而![]() ,
,![]() A错误;
A错误;
对于B,取![]() 、
、![]() 中点
中点![]() 、
、![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() ,
,
则![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
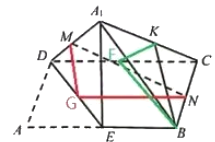
![]() ,
,![]() ,则四边形
,则四边形![]() 为梯形,且
为梯形,且![]() 、
、![]() 为底,
为底,
又![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,同理可得
,同理可得![]() 平面
平面![]() ,B选项错误;
,B选项错误;
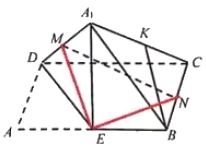
对于C,连接![]() 、
、![]() ,
,
当![]() 时,
时,![]() ,
,
而![]() ,
,![]() ,
,
![]() 与
与![]() 不垂直,即
不垂直,即![]() 不垂直平面
不垂直平面![]() ,C选项错误;
,C选项错误;
对于D,![]() 在以
在以![]() 为直径球面上,球心为
为直径球面上,球心为![]() ,
,
![]() 的轨迹为
的轨迹为![]() 外接圆(
外接圆(![]() 与
与![]() 不重合,
不重合,![]() 为
为![]() 的中点),
的中点),
连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
且![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,![]() .
.
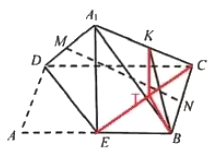
当直线![]() 与平面
与平面![]() 所成角取得最大值时,点
所成角取得最大值时,点![]() 到平面
到平面![]() 的距离最大,
的距离最大,
由于点![]() 为
为![]() 的中点,此时,点
的中点,此时,点![]() 到平面
到平面![]() 的距离最大,
的距离最大,
由于![]() ,当
,当![]() 与平面
与平面![]() 所成角最大时,点
所成角最大时,点![]() 到平面
到平面![]() 的距离最大.
的距离最大.
所以,直线![]() 、
、![]() 与平面
与平面![]() 所成角能同时取到最大值.
所成角能同时取到最大值.
故选:D.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目