题目内容
若函数f(x)在x=x0处的f'(x)=2,则| lim |
| k→0 |
| f(x0-k)-f(x0) |
| k |
分析:由导数定义可以直接得到结论,当割线的两个端点其中之一向另一个端点无限靠近时,其极限为固定端端点的导数
解答:解:
=-
=-f′(x0)
又函数f(x)在x=x0处的f'(x)=2,
∴
=-2
故答案为-2
| lim |
| k→0 |
| f(x0-k)-f(x0) |
| k |
| lim |
| k→0 |
| f(x0)-f(x0-k) |
| k |
又函数f(x)在x=x0处的f'(x)=2,
∴
| lim |
| k→0 |
| f(x0-k)-f(x0) |
| k |
故答案为-2
点评:本题考查极限及其运算,求解的关键有二,一是熟练掌握导数的定义,二是导数极限定义式的格式记忆准确,如此才能想到改变分子上两个函数式的顺序得出正确答案.此也是本题的一个易错点,极易出错,解决的办法就是对定义掌握准确.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
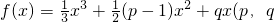 为常数).
为常数). 为常数).
为常数). 为常数).
为常数). ,则称函数f(x)在[a,b]上是下凸函数;有以下几个函数:
,则称函数f(x)在[a,b]上是下凸函数;有以下几个函数: ;
; ;
; .
.