题目内容
(本题满分16分)数列{an}中,![]() .
.
(Ⅰ)求a1,a2,a3,a4; (Ⅱ)猜想an的表达式,并用数学归纳法加以证明.
(本题满分16分)数列{an}中,![]() .
.
(Ⅰ)求a1,a2,a3,a4;(Ⅱ)猜想an的表达式,并用数学归纳法加以证明.
解:(Ⅰ)∵![]() ,∴
,∴![]() ,即a1=1………………………2分
,即a1=1………………………2分
∵![]() ,即a1+a2=4―a2―1,∴a3=1, …………………………4分
,即a1+a2=4―a2―1,∴a3=1, …………………………4分
∵![]() ,即a1+a2+a3=4―a3―
,即a1+a2+a3=4―a3―![]() ,∴a3=
,∴a3=![]() ,……………………………6分
,……………………………6分
∵![]() ,即a1+a2+a3+a4=4―a4―
,即a1+a2+a3+a4=4―a4―![]() ,∴a3=
,∴a3=![]() ,………………………8分
,………………………8分
(Ⅱ)猜想![]() …………………………………………………………………10分
…………………………………………………………………10分
证明如下:①当n=1时,a1=1,此时结论成立; ………………………………………12分
②假设当n=k(k∈N*)结论成立,即![]() ,
,
那么当n=k+1时,有![]()
![]()
![]()
![]() ,这就是说n=k+1时结论也成立.
,这就是说n=k+1时结论也成立.
综上所述,对任何n∈N*时![]() . ………………………………………16分
. ………………………………………16分
注:其它解法应参照给分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,令
,令 .
.  是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列? 中,
中, ,
,  为实常数),前
为实常数),前 项和
项和 恒为正值,且当
恒为正值,且当 时,
时, .
. 是等比数列;
是等比数列; 与
与 的等差中项为
的等差中项为 ,比较
,比较 的大小;
的大小; 是给定的正整数,
是给定的正整数, .现按如下方法构造项数为
.现按如下方法构造项数为 有穷数列
有穷数列 :
: 时,
时, ;
; 时,
时, .
. 的前
的前 .
.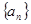 中,
中,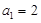 ,
,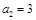 ,其前
,其前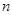 项和
项和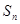 满足
满足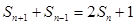 (
( ).
).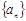 的通项公式;
的通项公式;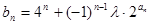 (
(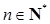 ),试确定非零整数
),试确定非零整数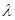 的值,使得对任意
的值,使得对任意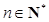 ,都有
,都有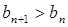 成立.
成立.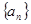 中,若
中,若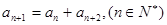 ,则称数列
,则称数列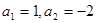 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;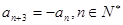 ;
;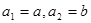 ,若数列
,若数列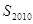 。
。 满足
满足 ,令
,令 .
.  是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求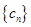 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列?