题目内容
已知三角形的三边长分别为 ,内切圆的半径为
,内切圆的半径为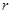 ,则三角形的面积为
,则三角形的面积为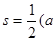
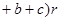 ;四面体的四个面的面积分别为
;四面体的四个面的面积分别为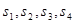 ,内切球的半径为
,内切球的半径为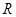 .类比三角形的面积可得四面体的体积为( )
.类比三角形的面积可得四面体的体积为( )
 ,内切圆的半径为
,内切圆的半径为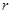 ,则三角形的面积为
,则三角形的面积为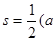
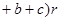 ;四面体的四个面的面积分别为
;四面体的四个面的面积分别为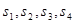 ,内切球的半径为
,内切球的半径为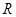 .类比三角形的面积可得四面体的体积为( )
.类比三角形的面积可得四面体的体积为( )A. | B. |
C. | D. |
C
解:设四面体的内切球的球心为O,
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
类比三角形的面积可得四面体的体积为: .
.
故选C
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
类比三角形的面积可得四面体的体积为:
 .
.故选C

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
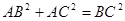 。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为 .
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为 .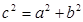 。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥
。设想正方形换成正方体,把截线换成如图所示的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥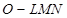 ,如果用
,如果用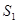 ,
,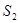 ,
,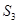 表示三个侧面面积,
表示三个侧面面积, 表示截面面积,那么你类比得到的结论是 。
表示截面面积,那么你类比得到的结论是 。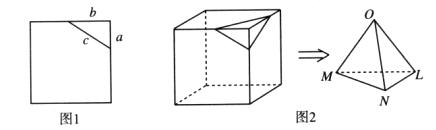
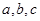 ,若
,若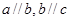 ,则
,则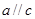 .类推出:向量
.类推出:向量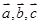 ,若
,若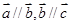 则
则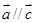
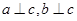 ,则
,则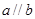 .类推出:空间中,三条不同的直线
.类推出:空间中,三条不同的直线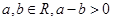 则
则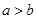 .类比出:任意
.类比出:任意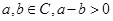 则
则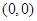 为圆心,
为圆心,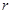 为半径的圆的方程是
为半径的圆的方程是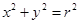 .类推出:以点
.类推出:以点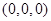 为球心,
为球心,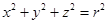
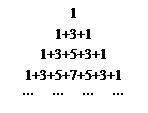
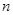 行
行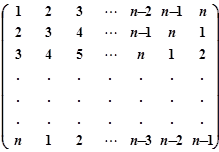
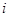 行第
行第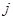 列的数为
列的数为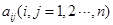 。
。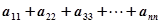 = ▲ ;(2分)
= ▲ ;(2分)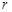 ,三边长为
,三边长为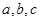 ,则三角形的面积等于
,则三角形的面积等于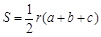 ,根据类比推理的方法,若一个四面体的内切球的半径为
,根据类比推理的方法,若一个四面体的内切球的半径为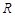 ,四个面的面积分别是
,四个面的面积分别是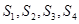 ,则四面体的体积
,则四面体的体积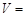 _____
_____  满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记这样的
成立,记这样的 ,则得到一个新数列
,则得到一个新数列 。例如,若数列
。例如,若数列 ,…,则数列
,…,则数列 , ….已知对任意的
, ….已知对任意的 ,则
,则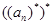 = 。
= 。