题目内容
在三棱锥A-BCD中，侧棱AB、AC、AD两两垂直，
、
、
的面积分别为
、
、
，则三棱锥A-BCD的外接球的体积为_______．
、、的面积分别为 、、，则三棱锥A-BCD的外接球的体积为_______．
试题分析：设侧棱AB、AC、AD长度分别为
，由三侧棱两两垂直，所以三棱锥的外接球是以三侧棱为临边的长方体的外接球，球的直径是长方体的体对角线，
，
点评：求解本题主要抓住关键点：侧棱AB、AC、AD两两垂直，这样就可得到三棱锥与长方体的关系，将三棱锥外接球转化为长方体外接球
练习册系列答案
名校课堂系列答案
相关题目
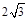,则其外接球的表面积为 . 
、
、
、
四点，若
，则四面体
的体积的取值范围是
，
，则棱锥S—ABC的体积为( )
