题目内容
是否存在实数a,使函数f(x)=log2(x+
)-a为奇函数,同时使函数g(x)=x(
+a)为偶函数,证明你的结论.
| x2+2 |
| 1 |
| ax-1 |
f(x)为奇函数,所以f(0)=0,
得log2
-a=0?a=
.
若g(x)为偶函数,则h(x)=
+a为奇函数,
h(-x)+h(x)=0?
+a+
+a=0
?2a=
-
?2a=1?a=
∴存在符合题设条件的a=
.
得log2
| 2 |
| 1 |
| 2 |
若g(x)为偶函数,则h(x)=
| 1 |
| ax-1 |
h(-x)+h(x)=0?
| 1 |
| a-x-1 |
| 1 |
| ax-1 |
?2a=
| ax |
| ax-1 |
| 1 |
| ax-1 |
| 1 |
| 2 |
∴存在符合题设条件的a=
| 1 |
| 2 |

练习册系列答案
相关题目
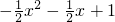 ,f3(x)=2x-1,f4(x)=cosx.;
,f3(x)=2x-1,f4(x)=cosx.;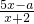 在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.
在D2上封闭,若存在,求出a的值,并给出证明,若不存在,说明理由.