题目内容
设函数f(x)=cos2x+asinx-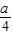 -
- .
.(1)当 0≤x≤
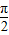 时,用a表示f(x)的最大值M(a);
时,用a表示f(x)的最大值M(a);(2)当M(a)=2时,求a的值,并对此a值求f(x)的最小值;
(3)问a取何值时,方程f(x)=(1+a)sinx在[0,2π)上有两解?
【答案】分析:(1)用同角公式对f(x)化简得f(x)=-sin2x+asinx+1-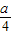 -
- ,设sinx=t,则函数g(t)是开口向下,对称轴为t=
,设sinx=t,则函数g(t)是开口向下,对称轴为t=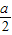 的抛物线,根据二次函数的性质,对a进行讨论得出答案.
的抛物线,根据二次函数的性质,对a进行讨论得出答案.
(2)M(a)=2代入(1)中的M(a)的表达式即可得出结果.
(3)方程f(x)=(1+a)sinx.即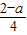 =sin2x+sinx,x∈[0,2π)欲使方程f(x)=(1+a)sinx在[0,2π)上有两解.则必须
=sin2x+sinx,x∈[0,2π)欲使方程f(x)=(1+a)sinx在[0,2π)上有两解.则必须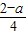 ∈(0,2)∪{-
∈(0,2)∪{- },从而求出a的范围即可.
},从而求出a的范围即可.
解答:解:(1)f(x)=-sin2x+asinx+1-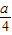 -
- ,
,
∵0≤x≤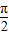
∴0≤sinx≤1
令sinx=t,则f(t)=-t2+at+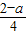 ,t∈[0,1]
,t∈[0,1]
∴M(a)=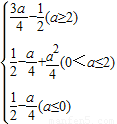 .
.
(2)当M(a)=2时,
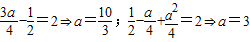 或a=-2(舍);
或a=-2(舍);
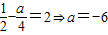 .
.
∴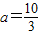 或a=-6.
或a=-6.
①当a=-6时,f(x)min=-5;
②当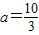 时,f(x)min=-
时,f(x)min=- .
.
(3)方程f(x)=(1+a)sinx
即-sin2x+asinx+1-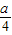 -
- =(1+a)sinx,
=(1+a)sinx,
即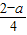 =sin2x+sinx,x∈[0,2π)
=sin2x+sinx,x∈[0,2π)
∵sin2x+sinx∈[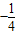 ,2],
,2],
∵方程f(x)=(1+a)sinx在[0,2π)上有两解.
∴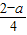 ∈(0,2)∪{-
∈(0,2)∪{- },
},
∴-6<a<2或a=3.
点评:本题主要考查了三角函数恒等变换的应用和二次函数的性质.在二次函数的性质的使用的时候要特别注意对称轴的位置.
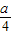 -
- ,设sinx=t,则函数g(t)是开口向下,对称轴为t=
,设sinx=t,则函数g(t)是开口向下,对称轴为t=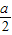 的抛物线,根据二次函数的性质,对a进行讨论得出答案.
的抛物线,根据二次函数的性质,对a进行讨论得出答案.(2)M(a)=2代入(1)中的M(a)的表达式即可得出结果.
(3)方程f(x)=(1+a)sinx.即
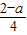 =sin2x+sinx,x∈[0,2π)欲使方程f(x)=(1+a)sinx在[0,2π)上有两解.则必须
=sin2x+sinx,x∈[0,2π)欲使方程f(x)=(1+a)sinx在[0,2π)上有两解.则必须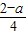 ∈(0,2)∪{-
∈(0,2)∪{- },从而求出a的范围即可.
},从而求出a的范围即可.解答:解:(1)f(x)=-sin2x+asinx+1-
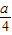 -
- ,
,∵0≤x≤
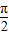
∴0≤sinx≤1
令sinx=t,则f(t)=-t2+at+
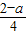 ,t∈[0,1]
,t∈[0,1]∴M(a)=
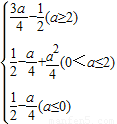 .
.(2)当M(a)=2时,
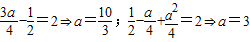 或a=-2(舍);
或a=-2(舍);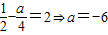 .
.∴
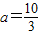 或a=-6.
或a=-6.①当a=-6时,f(x)min=-5;
②当
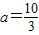 时,f(x)min=-
时,f(x)min=- .
.(3)方程f(x)=(1+a)sinx
即-sin2x+asinx+1-
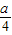 -
- =(1+a)sinx,
=(1+a)sinx,即
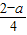 =sin2x+sinx,x∈[0,2π)
=sin2x+sinx,x∈[0,2π)∵sin2x+sinx∈[
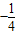 ,2],
,2],∵方程f(x)=(1+a)sinx在[0,2π)上有两解.
∴
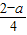 ∈(0,2)∪{-
∈(0,2)∪{- },
},∴-6<a<2或a=3.
点评:本题主要考查了三角函数恒等变换的应用和二次函数的性质.在二次函数的性质的使用的时候要特别注意对称轴的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目