题目内容
各项都为正数的数列
中，
猜想数列的通项
A． | B． | C． | D． |
A
解析试题分析：根据题意发现规律可知，由于数列的前4项由规律，后面的一项是总是比前一项多个常数，并且规律为
，然后利用累加法来求解数列的通项公式，得到结论，故为
，故答案选A.
考点：数列的通项公式
点评:解决的关键是利用数列的前几项来分析得到其通项公式，属于基础题。
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
相关题目
一个等比数列
的前n项和为48，前2n项和为60，则前3n项和为（ ）
| A．108 | B．63 | C．75 | D．83 |
等比数列
中，已知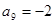
，则此数列前17项之积为（ ）
A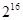． | B． | C． | D． |
等比数列{
}中，若
，则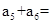
（ ）
| A．2 | B．40 | C．80 | D．120 |
等比数列{an}中，a2＝9，a5＝243，则{an}的前4项和为( ).
| A．81 | B．120 | C．168 | D．192 |
在等比数列{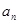
}中，若
，
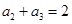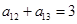，则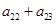
的值是（ ）
A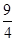． | B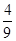． | C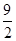． | D． |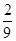
已知等比数列{an}公比为q，其前n项和为Sn，若S3，S9，S6成等差数列，则q3等于
A．- | B．1 | C．-或1 | D．-1或 |
等比数列{an}中，a7=10，q=-2,则a10 =（ ）
| A．4 | B．40 | C．80 | D．-80 |
已知等比数列
中，有
，数列
是等差数列，且
，则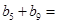
（ ）
| A．2 | B．4 | C．8 | D．16 |