题目内容
7.(1)若复数z满足(1+i)z=2-i,求|z+i|.(2)已知函数f(x)=x4+x2-1,g(x)=ax3+x2+b(x∈R),其中a,b∈R.
设F(x)=f(x)+g(x),若对于任意的a∈[-2,2],函数y=F(x)在区间[-1,1]上的值恒为负数,求b的取值范围.
分析 (1)利用复数的运算法则及模的计算公式即可得出;
(2)F(x)=f(x)+g(x)=x4+ax3+2x2+b-1,由函数y=F(x)在区间[-1,1]上的值恒为负数,可得x4+ax3+2x2+b-1<0,即b<-x4-ax3-2x2+1=h(x),x∈[-1,1].利用导数研究函数h(x)的单调性与极值最值即可得出.
解答 解:(1)∵复数z满足(1+i)z=2-i,∴z=$\frac{2-i}{1+i}$=$\frac{(2-i)(1-i)}{(1+i)(1-i)}$=$\frac{1-3i}{2}$,∴z+i=$\frac{1}{2}-\frac{1}{2}i$.
∴|z+i|=$\sqrt{(\frac{1}{2})^{2}+(-\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$.
(2)F(x)=f(x)+g(x)=x4+ax3+2x2+b-1,
∵函数y=F(x)在区间[-1,1]上的值恒为负数,
∴x4+ax3+2x2+b-1<0,即b<-x4-ax3-2x2+1=h(x),x∈[-1,1].
h′(x)=-4x3-3ax2-4x=-4x$({x}^{2}+\frac{3}{4}ax+1)$,
对于一元二次方程:${x}^{2}+\frac{3}{4}ax+1$=0,∵a∈[-2,2],
∴△=$\frac{9}{16}{a}^{2}$-4<0.
∴?x∈[-1,1],${x}^{2}+\frac{3}{4}ax+1$>0恒成立.
令h′(x)>0,解得-1≤x<0,此时函数h(x)单调递增;令h′(x)<0,解得0<x≤1,此时函数h(x)单调递减.
又h(-1)=a-2,h(1)=-a-2,
∴h(x)min={a-2,-a-2}min,
∴b<{a-2,-a-2}min,a∈[-2,2].
点评 本题考查了利用导数研究函数的单调性极值与最值、复数的运算法则及模的计算公式,考查了分类讨论、推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{25}{3}$ | B. | $\frac{50}{9}$ | C. | 7 | D. | 6 |
| A. | -1 | B. | 1 | C. | -1或1 | D. | 0或-1或1 |
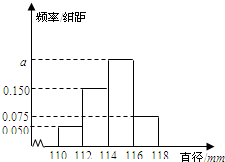 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118]内该厂可获利分别为10,30,20,10(单位:元),现从该厂生产的产品A中随机抽取200件测量它们的直径,得到如图所示的频率分布直方图.