题目内容
(选做题)
设函数f(x)=|x-1|,g(x)=|x-2|,
(Ⅰ)解不等式f(x)+g(x)<2;
(Ⅱ)对于实数x,y,若f(x)≤1,g(y)≤1,求证|x-2y+3|≤3。
设函数f(x)=|x-1|,g(x)=|x-2|,
(Ⅰ)解不等式f(x)+g(x)<2;
(Ⅱ)对于实数x,y,若f(x)≤1,g(y)≤1,求证|x-2y+3|≤3。
解:(1)令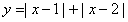 ,
,
则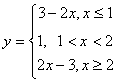 ,
,
作出函数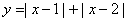 的图象,
的图象,
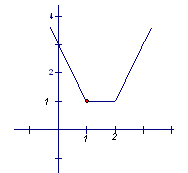
它与直线y=2的交点为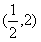 和
和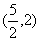 ,
,
所以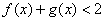 的解集为
的解集为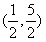 。
。
(2)因为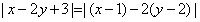
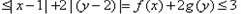 ,
,
所以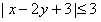 。
。
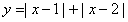 ,
,则
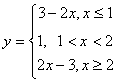 ,
,作出函数
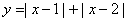 的图象,
的图象,
它与直线y=2的交点为
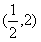 和
和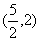 ,
,所以
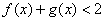 的解集为
的解集为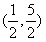 。
。(2)因为
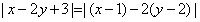
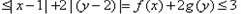 ,
, 所以
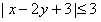 。
。
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
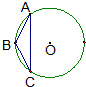 短长度为
短长度为 (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)