题目内容

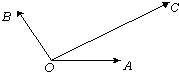如图，在平面内有三个向量
OA
，
OB
，
OC
，满足|
OA
|=|
OB
|=1，
OA
与
OB
的夹角为120°，
OC
与
OA
的夹角为30°，|
OC
|=5
3
，设
OC
=m
OA
+n
OB
（m，n∈R，则m+n等于（　　）
分析：利用平面向量的基本定理、向量垂直与数量积的关系及|
a
|=
a
2
即可得出．
解答：解：如图所示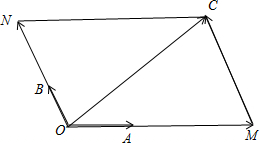，过点C分别作CM∥OB，CN∥OA，分别交射线OA、OB于M、N．
则
OC
=
OM
+
ON
=m
OA
+n
OB
．
∵∠AOB=120°，∠AOC=30°，∴∠OCM=90°．
∴
OC
•
MC
=0=(m
OA
+n
OB
)•(n
OB
)，化为mcos120°+n=0，即m=2n．
又|
OC
|=5
3
，∴(5
3
)2=(m
OA
+n
OB
)2，
∴75=m2+n2+2mncos120°，化为m2+n2-mn=75．
联立
m=2n
m2+n2-mn=75
，由图可知，m＞0，n＞0．解得
m=10
n=5
．
∴m+n=15．
故选D．
点评：熟练掌握平面向量的基本定理、向量垂直与数量积的关系及|
a
|=
a
2
是解题的关键．
练习册系列答案
相关题目
70、在平面内，如果用一条直线去截正方形的一个角，那么截下的一个直角三角形按图1所标边长，由勾股定理有：c2=a2+b2．设想正方形换成正方体，把截线换成如图2所示的截面，这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN，如果用S1，S2，S3表示三个侧面面积，S4表示截面面积，那么你类比得到的结论是
S42=S12+S22+S32
．
如图，某海面上有O、A、B三个小岛（面积大小忽略不计），A岛在O岛的东北方向20
2
km处，B岛在O岛的正东方向10km处．
（1）以O为坐标原点，O的正东方向为x轴正方向，1km为单位长度，建立平面直角坐标系，试写出A、B的坐标，并求A、B两岛之间的距离；
（2）已知在经过O、A、B三个点的圆形区域内有未知暗礁，现有一船在O岛的南偏西30°方向距O岛20km处，正沿东北方向行驶，若不改变方向，试问该船有没有触礁的危险？
（2013•湖南）在平面直角坐标系xOy中，将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”．如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”．某地有三个新建居民区，分别位于平面xOy内三点A（3，20），B（-10，0），C（14，0）处．现计划在x轴上方区域（包含x轴）内的某一点P处修建一个文化中心．
（I）写出点P到居民区A的“L路径”长度最小值的表达式（不要求证明）；
（II）若以原点O为圆心，半径为1的圆的内部是保护区，“L路径”不能进入保护区，请确定点P的位置，使其到三个居民区的“L路径”长度之和最小．

如图，在平面内有三个向量，，满足=1，，与的夹角为120°，与的夹角为30°，设∈R)则的值为

A．1                         B．                   C．10                       D．15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网